Courbes et Tangentes dans les Mathématiques Grecques I

Ce que nous avons des Anciens sur ces matières, principalement d'Archimède, est assurément digne d'admiration. Mais outre qu'ils n'ont touché qu'à fort peu de courbes, qu'ils n'y ont même touché que légèrement ; ce ne sont presque partout que propositions particulières et sans ordre, qui ne font apercevoir aucune méthode régulière et suivie. Ce n'est pas cependant qu'on leur en puisse faire un reproche légitime : ils ont eu besoin d'une extrême force de génie pour percer à travers tant d'obscurités, et pour entrer les premiers dans des pays entièrement inconnus.
Guillaume De L'Hospital : préface de l'analyse des infiniment petits.


Les acteurs principaux

Le cercle : Euclide

La première définition de la notion de tangence qui nous soit parvenue se trouve au début du livre III des Eléments d'Euclide, livre qui est consacré aux propriétés du cercle :

Définition 2 : Une droite qui, rencontrant un cercle et prolongée, ne le coupe pas, est dite être tangente au cercle.
Définition 3 : Des cercles qui se rencontrent l'un l'autre sans se couper, sont dits être tangents l'un à l'autre. ([EUC], t.1, p.387)

Note sur les Eléments d'Euclide : Montrer

Quelques pages plus loin la proposition III.16 donne une caractérisation de la tangente à un cercle en termes de convexité et vient préciser la nature du contact entre le cercle et sa tangente :

La droite menée à angles droits avec le diamètre du cercle à partir d'une extrémité tombera à l'extérieur du cercle, et dans le lieu compris entre la droite et la circonférence, une autre droite ne sera pas intercalée ; en outre, d'une part l'angle du demi-cercle est plus grand, d'autre part l'angle restant plus petit, que tout angle rectiligne aigu. ([EUC], t.1, p.423-424)

Commentaire : Dans la figure 1, la droite AE, perpendiculaire au diamètre AB, est située entièrement à l'extérieur du cercle.
L'impossibilité d' « intercaler une autre droite » entre le cercle et sa tangente en un de ses points A caractérise la tangente parmi toutes les droites passant par A. Cette propriété reste vraie pour la tangente à une courbe quelconque. A la fin du 18e siècle, Joseph Louis Lagrange reprendra et développera cette idée pour en faire une théorie du contact de deux courbes.
"L'angle du demi-cercle" est l'angle (mixtiligne) formé par le diamètre AB et l'arc AC ; il est "plus grand" que l'angle BAZ. "L'angle restant" est l'angle (mixtiligne) formé par l'arc AC et la demi droite AE ; il est "plus petit" que l'angle ZAE.

Euclide en déduit immédiatement le corollaire :

Alors, à partir de ceci, il est évident que la droite menée à angles droits avec le diamètre d'un cercle à partir d'une extrémité est tangente au cercle (et que la droite touche le cercle en un point seulement puisqu'il a été aussi démontré que celle qui le rencontre en deux points tombe à l'intérieur). ([EUC], t.1, p.425)

On voit qu'à cette occasion, Euclide utilise la notion surprenante d'angle d'un segment circulaire qu'il a défini au début du livre III comme l'angle (mixtiligne) formé par la circonférence d'un cercle et l'une de ses cordes. On peut y voir un exemple de grandeur non archimédienne envisagée par les Grecs.

Définition d'une grandeur archimédienne : Montrer

La définition d'Euclide d'une droite tangente à un cercle pouvait être étendue aux différentes courbes connues des mathématiciens grecs. C'est en effet ce qu'ils firent lors de leur étude des tangentes aux coniques et à la spirale. Dans les Eléments, la notion de tangence n'est pas utilisée dans d'autres cas que celui du cercle, mais, selon le témoignage de Pappus d'Alexandrie, Euclide aurait également rédigé quatre livres sur les coniques. Ceux-ci ne nous sont malheureusement pas parvenus, mais d'après Heath (cf [5], p.116-126) ils devaient contenir les propriétés élémentaires des tangentes aux coniques.

La parabole : Archimède

Au début du traité d'Archimède la quadrature de la parabole, figurent trois propositions concernant les tangentes à la parabole qui nous donnent des indications précieuses sur les connaissances des mathématiciens grecs de cette époque relatives à ce sujet. On remarquera à la fin de l'extrait l'allusion à des Eléments relatifs aux sections coniques dont l'auteur n'est pas mentionné ce qui a entrainé nombre d'hypothèses sur son identité de la part des historiens (cf [5], p.116-126 et [8]).

Proposition I : Si l'on a une parabole, sur laquelle se trouve l'arc ABC, une droite BD parallèle au diamètre (i.e. l'axe de la parabole), ou diamètre elle­ même, une droite AC parallèle à la tangente à la parabole en B, la droite AD sera égale à la droite DC,(i.e. les segments AD et DC auront même longueur) et, si la droite AD est égale à la droite DC, la droite AC et la tangente à la parabole en B seront parallèles.(cf. figure 2)
Proposition II : Si ABC est une parabole, la droite BD une parallèle au diamètre, ou diamètre elle-même, la droite ADC une parallèle à la tangente à la parabole au point B, et si la droite EC est une tangente à la parabole au point C, les droites BD, BE seront égales.(cf. figure 3)
Proposition III : Si ABC est une parabole, la droite BD une parallèle au diamètre, ou le diamètre même, et, si des droites AD, EZ sont menées parallèlement à la tangente à la parabole au point B, le carré de la droite AD sera au carré de la droite EZ comme la droite BD est à la droite BZ (cf. figure 4). Ces propositions sont d'ailleurs démontrées dans les Eléments relatifs aux sections coniques. ([ARC], t.2, p. 378-379)

Commentaire : La conclusion de la proposition III signifie que AD² : EZ² = BD : BZ. Cette relation métrique qui caractérise les points de la parabole est l'équivalent de notre équation : y² = kx.

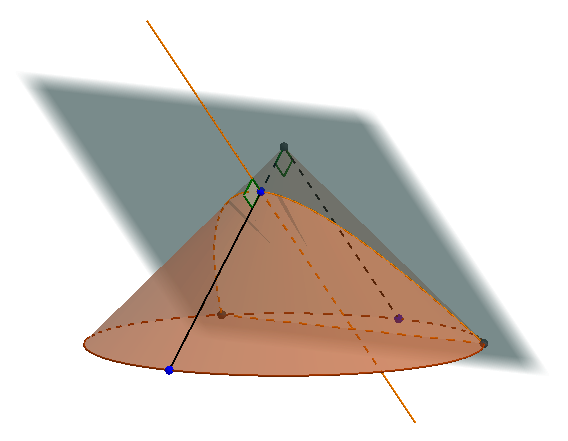
Il est bon de préciser que pour Archimède une parabole était la section droite (i.e. la section par un plan perpendiculaire à une génératrice) d'un cône dont l'angle au sommet est droit (cf. figure ci-dessous).

En effet, avant Apollonius, un cône était la figure obtenue par rotation d'un tour complet d'un triangle rectangle autour d'un de ses côtés perpendiculaires (Euclide, 11ème élément, déf.18) et les coniques étaient obtenues comme section droite de trois sortes de cônes selon que l'angle au sommet était aigu, droit ou obtus.

Animation section droite d'un cône : Montrer

Les coniques : Apollonius

Nous ne disposons d'aucun élément biographique certain sur Apollonius. Selon la tradition il serait né vers 262 avant notre ère à Perga, une ville d'Asie Mineure, et aurait étudié à Alexandrie avec les successeurs d'Euclide. Il aurait séjourné dans cette ville une grande partie de sa vie et serait décédé aux environs de 190 avant notre ère.

Sa renommée repose sur son traité des sections coniques qui comportait huit livres dont seuls les sept premiers nous sont parvenus. Dans ce traité, Apollonius redéfinit les coniques comme section plane d'une même "surface conique" par des plans d'inclinaison variable. Par "surface conique" Apollonius entend la surface engendrée par une droite passant par un point fixe (le sommet) et par un point variable décrivant un cercle situé dans un plan ne contenant pas le sommet (Livre I, déf.1). Cette nouvelle définition lui permet de considérer les deux branches de l'hyperbole comme une section unique. Nous devons également à Apollonius l'emploi des mots ellipse, parabole et hyperbole pour désigner les trois types de coniques.

Animation section plane d'un cône de révolution : Montrer

En rapportant la conique à un diamètre quelconque et à ses cordes conjuguées, Apollonius établit l'existence d'une relation métrique caractéristique de chaque type de conique. Si nous interprétions, de manière anachronique, ces relations en termes de coordonnées dans un repère ayant pour origine un point de la conique et pour directions le diamètre correspondant à ce point et son diamètre conjugué, celles ci pourraient s'écrire avec les notations habituelles :

Y² = 2pX dans le cas de la parabole ;
Y² = 2pX - pX²/a pour l'ellipse ;
Y² = 2pX + pX²/a pour l'hyperbole.

Prenons par exemple le cas de l'ellipse. Un diamètre de l'ellipse est une droite passant par son centre (telle (AB) dans la figure 6). Les tangentes à l'ellipse en ses points d'intersection avec un diamètre sont parallèles. Le diamètre conjugué est parallèle à ces tangentes (dans la figure 6 (CD) est parallèle aux tangentes en A et en B et CD est une demi corde conjuguée). Apollonius démontre que le rapport CD² : AC×CB est constant (= k). Si l'on pose AB = 2a, p = ka, AC = x et CD = y, on obtient la relation y² = 2px - px²/a .

Lorsque l'on compare les quantités Y² et 2pX, il y a un manque dans le cas de l'ellipse (c'est le sens du mot grec ελλειψις) et un excès dans celui de l'hyperbole (c'est le sens du mot grec υπερβολη).

Voici un extrait du premier livre dans lequel Apollonius démontre la réciproque de la proposition II du traité de la parabole d'Archimède. Pour prouver qu'une certaine droite est tangente à la parabole, Apollonius montre par un raisonnement par l'absurde que la droite reste toujours à l'extérieur de la parabole, ce qui correspond bien à la définition de la tangente donnée par Euclide. (Pour la compréhension du texte nous rappelons qu'un diamètre est une droite parallèle à l'axe de la parabole ; que le sommet est le point d'intersection du diamètre avec la parabole ; que les droites abaissées de manière ordonnée ont toutes la même direction qui est celle de la tangente au sommet de la parabole.)

Proposition XXXIII : Si l'on prend un point sur une parabole ; si, de ce point, l'on abaisse une droite d'une manière ordonnée sur le diamètre, et si l'on pose une droite égale à celle que cette dernière droite découpe sur le diamètre, dans la direction de celui-ci, et à partir du sommet, la droite de jonction, menée du point ainsi obtenu au point que l'on a pris, sera tangente à la section.

La signification de ce paragraphe s'éclaire à la lecture du suivant : E est le milieu du segment AD et la droite AC est tangente en C à la parabole (cf. figure 7).

Soit une parabole dont un diamètre est la droite AB. Abaissons une droite CD de manière ordonnée ; posons une droite AE égale à la droite ED, et menons la droite de jonction AC. Je dis que la droite AC prolongée tombera à l'extérieur de la section.
En effet, qu'elle tombe à l'intérieur comme la droite CZ, et abaissons la droite HB de manière ordonnée. Dés lors, puisque le rapport du carré de BH au carré de CD est plus grand que celui du carré de ZB au carré de CD ; mais que le carré de BA est au carré de AD comme le carré de ZB est au carré de CD ; et que BE est à DE comme le carré de HB est au carré de CD, il s'ensuit que le rapport de BE à ED est plus grand que celui du carré de BA au carré de AD.

Commentaire : HB² ÷ CD² > ZB² ÷ CD² (Z est à l'intérieur de la parabole entre B et H), AB² ÷ AD² = ZB² ÷ CD² (les triangles ADC et ABZ sont semblables) et HB² ÷ CD² = BE ÷ DE (relation caractéristique de la parabole) donc BE ÷ DE > AB² ÷ AD².

Or, le quadruple du rectangle délimité sous BE, EA est au quadruple du rectangle délimité sous AE, ED comme BE est à ED ; donc le rapport du quadruple du rectangle délimité sous BE, EA au quadruple du rectangle délimité sous AE, ED est plus grand que celui du carré de BA au carré de AD. Dès lors, par permutation, le rapport du quadruple du rectangle délimité sous BE, EA au carré de AB est plus grand que celui du quadruple du rectangle délimité sous AE, ED au carré de AD ;

Commentaire : (4 × AE × BE) ÷ (4 × AE × DE) > BA² ÷ AD² donc (4 × AE × BE) ÷ BA² > (4 × AE × DE)  ÷ AD²

ce qui ne peut avoir lieu, car, ED étant égal à AE, le quadruple du rectangle délimité sous AE, ED équivaut au carré de AD, et le quadruple du rectangle délimité sous BE, EA est moindre que le carré de BA , puisque le point E n'est pas le milieu de la droite AB. Dès lors, la droite AC ne tombe pas à l'intérieur de la section ; donc lui est tangente. ([APO] livre1 prop.33)

Commentaire : 4 × AE × DE  = AD² et 4 × AE × BE < BA² car le produit AE × BE est maximal lorsque E est au milieu du segment AB ; en effet de tous les rectangles de périmètre donné celui qui a l'aire maximale est le carré.

Il faut noter qu'Apollonius traite séparément la réciproque de la cette propriété XXXIII puisque c'est l'objet de la proposition XXXV (Si la droite AC est tangente à la parabole en C alors AE = ED en gardant les notations de la figure 7). Le choix de l'ordre d'exposition de ces propositions n'est pas anodin, en effet c'est la proposition XXXIII qui assure de l'existence de la tangente.

Dans le cas de l'ellipse et de l'hyperbole qu'il traite simultanément (proposition XXXIV et XXXVI pour la réciproque), Apollonius démontre que la tangente et l'ordonnée passant par le point de contact coupent harmoniquement le diamètre ( Dans les figures 8 et 8bis (A, B, C, T) forment une division harmonique ).

Signalons pour finir un autre résultat remarquable démontré également par Apollonius dans la suite de son traité : la tangente à l'ellipse détermine le même angle avec chacune des droites reliant le point de contact avec les foyers. ( Dans la figure 9, F et F' sont les foyers de l'ellipse, la droite tt' est tangente en D à l'ellipse et les angles FDt et F'Dt' sont égaux. )

Bibliographie

    Autres ouvrages

  1. Bettinelli Bernard. Le trésor d'Archimède. IREM de Besançon, 1988.
  2. Collectif. Le matin des mathématiciens. Belin-Radio France 1985.
  3. Deleham Ph., Kientz G., Penin J.C., Perrin P. Histoire de tangentes. IREM de Reims, 1994.
  4. Dhombres Jean.Nombre, mesure et continu. Cedic/Fernand Nathan, 1978.
  5. Heath Thomas Sir. A history of greeks mathematics vol2. Oxford, Clarendon Press, 1921.
  6. Zeuthen Hieronymus Georg. Histoire des mathématiques dans l'antiquité et le moyen-âge éd. française. Gauthier-Villars, Paris 1902

    7. Articles en ligne

  7. Trotoux Didier. Résumé du livre I des coniques d'Apollonius. www.math.unicaen.fr/irem/spip.php?article151
  8. Vitrac Bernard. Apollonius de Perge et la tradition des coniques. culture.ens.fr/histoire des maths/htm/Vitrac/grec-8.html
Image de fond : source gallica.bnf.fr/BnF