Courbes et tangentes au 17e siècle
3. La méthode de Fermat
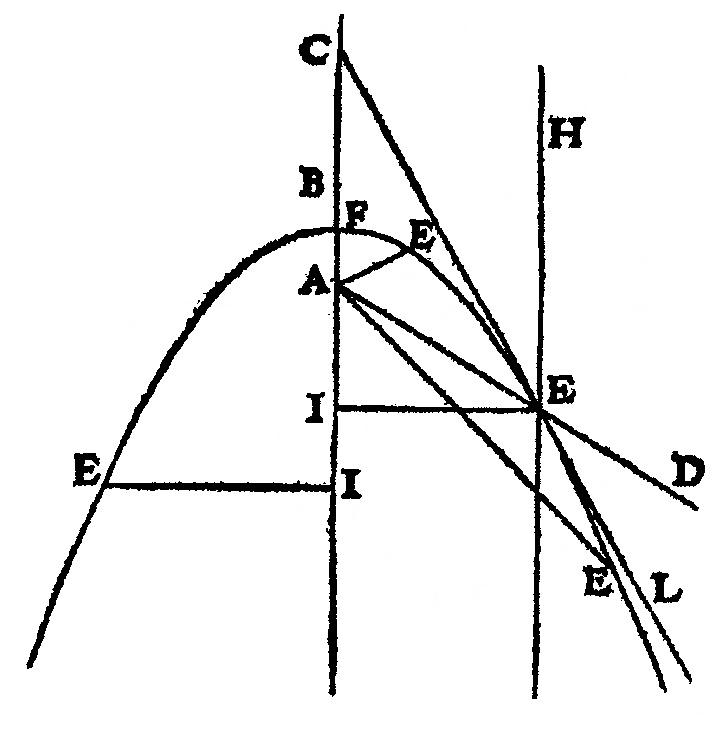
Pierre de Fermat est l'auteur de la première méthode analytique de calcul de la tangente. Il expose sa méthode pour la recherche du maximum et du minimum pour la première fois en 1638 puis la précise dans cinq autres textes.
Courbes et tangentes au 17e siècle
2. La méthode de Descartes
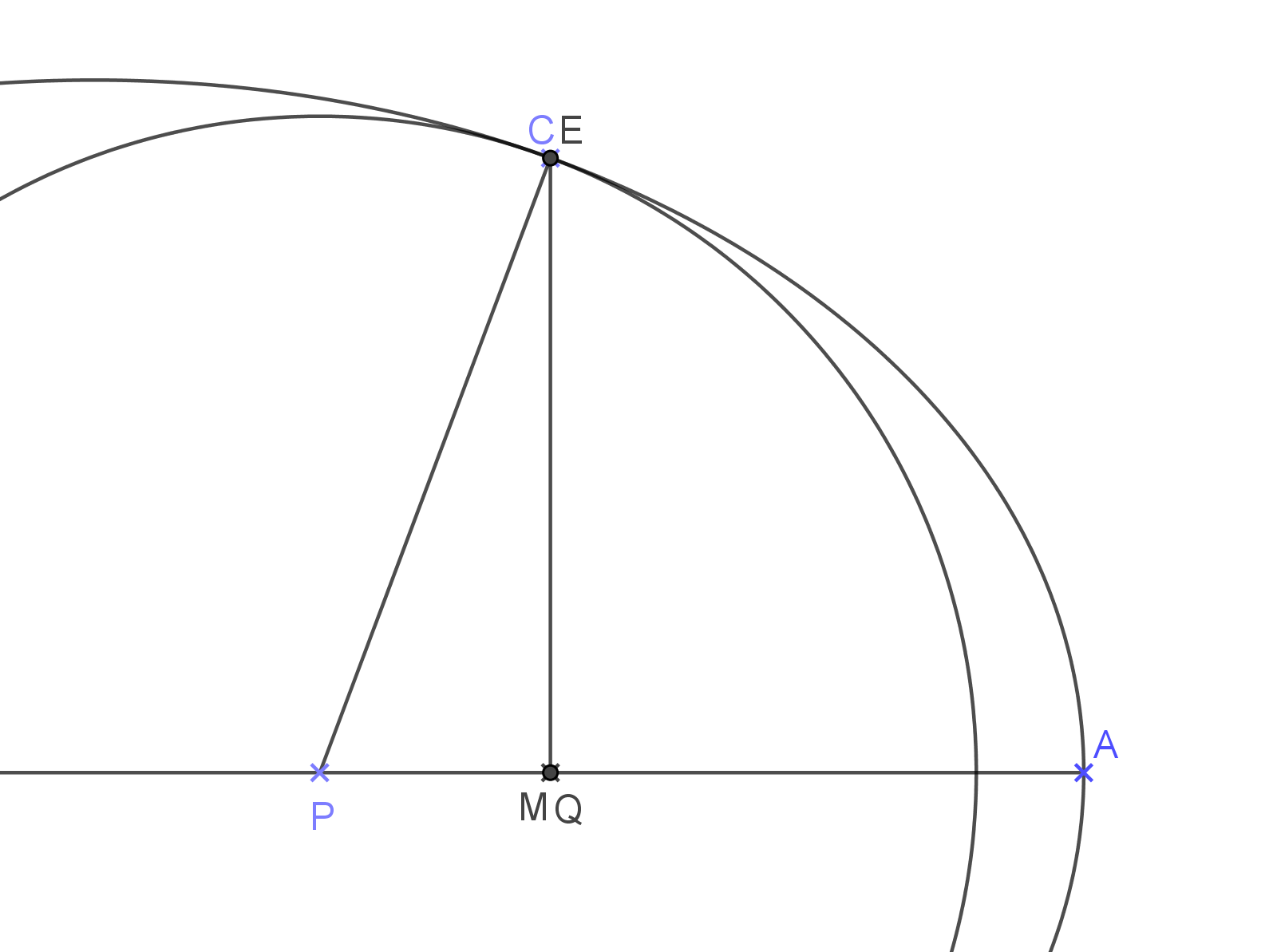
René Descartes est l'initiateur des méthodes algébriques de calcul de la tangente. Il expose sa première méthode utilisant les points d'intersection de la courbe avec un cercle de rayon variable dans son ouvrage La Géométrie publié en 1637.
Courbes et tangentes au 17e siècle
1. La méthode de Roberval
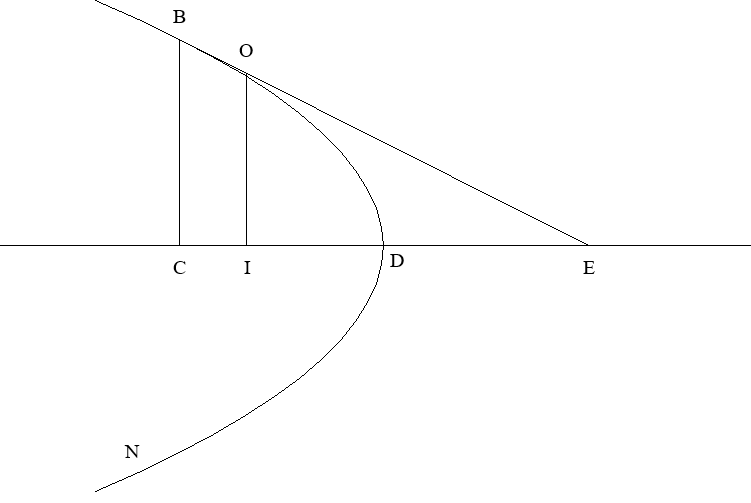
Dans le second quart du 17e siècle vont éclore nombre de méthodes originales de détermination de la tangente. Celle de Gilles Personne de Roberval repose sur le principe de la composition des mouvements. Cet article présente cette méthode cinématique et l'utilisation qu'en fait Roberval pour déterminer les tangentes aux coniques et à la conchoïde de Nicomède.
Courbes et tangentes dans les mathématiques grecques (partie 2)
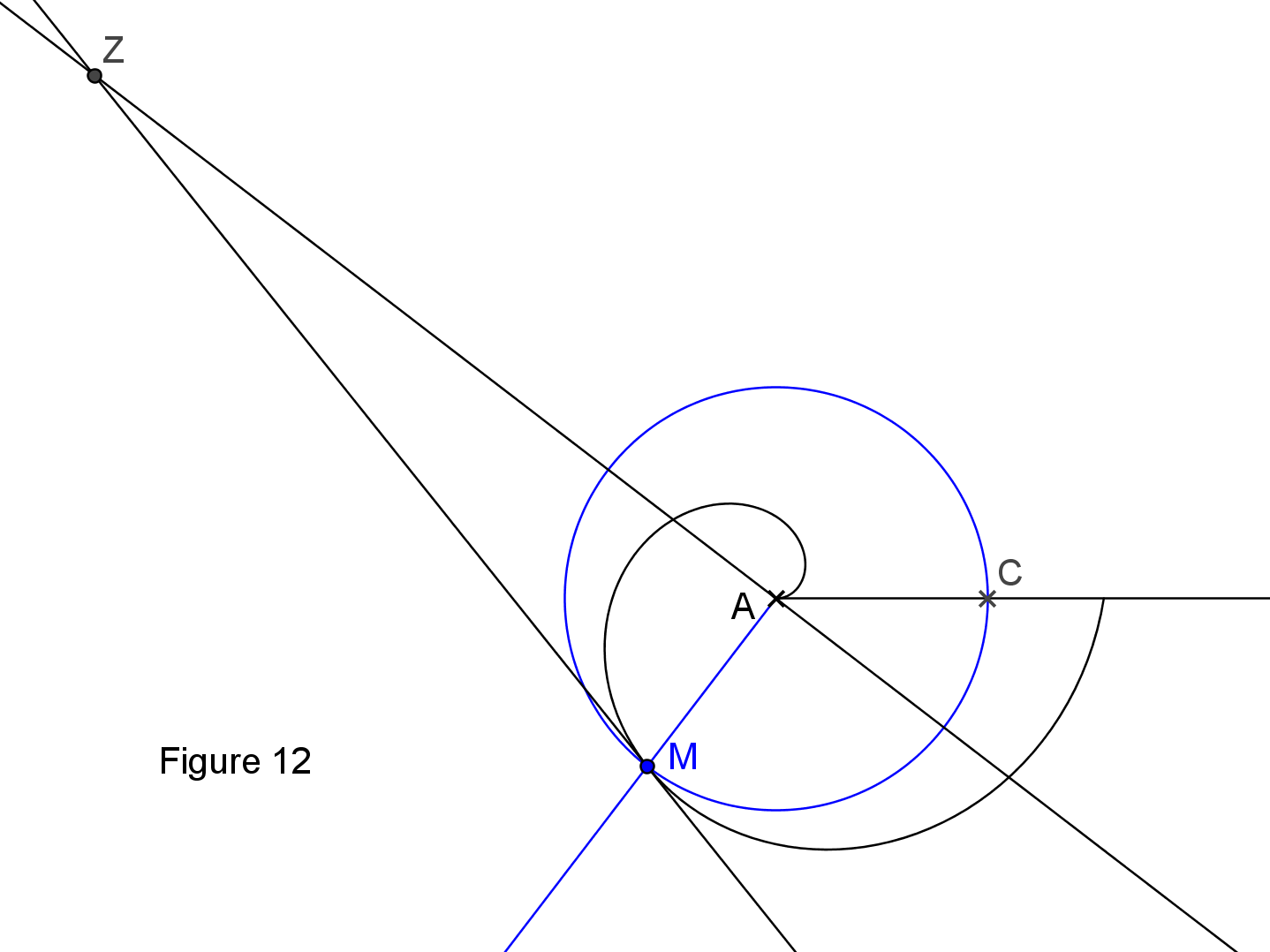
Dans cette seconde partie sont présentées quatre autres courbes étudiées par les mathématiciens grecs : la spirale d'Archimède avec la détermination de ses tangentes ; la conchoïde de Nicomède, la cissoïde de Dioclès et la quadratrice de Dinostrate avec leurs applications aux problèmes de construction.
Courbes et tangentes dans les mathématiques grecques (partie 1)
L'étude des tangentes à une courbe commence avec les mathématiciens grecs. Afin de montrer comment ceux-ci abordèrent le problème, sont présentés dans cette première partie quelques extraits de textes d'Archimède et d'Apollonius. Ils traitent de propriétés élémentaires des tangentes aux coniques.
L'équation de Pell Fermat et les mathématiques indiennes
Dix siècles avant que les mathématiciens européens ne commencent à s'y intéresser, le grand savant indien Brahmagupta avait étudié cette équation et donné ses solutions dans plusieurs cas.