Courbes et tangentes au 17e siècle

Chapitre 2 : La méthode de Descartes

C'est pourquoi je croirai avoir mis ici tout ce qui est requis pour les éléments des lignes courbes, lorsque j'aurai généralement donné la façon de tirer des lignes droites, qui tombent à angles droits sur tels de leurs points qu'on voudra choisir. Et j'ose dire que c'est ceci le problème le plus utile, et le plus général non seulement que je sache, mais même que j'aie jamais désiré de savoir en Géométrie.
Descartes : La Géométrie

Dans les méthodes algébriques le critère de contact de deux courbes est la coïncidence de deux points d'intersection : étant donnés une courbe C et un point fixe A de cette courbe, une ligne quelconque variable (droite ou cercle par exemple), qui coupe la courbe C en A et en un second point variable M, devient tangente à la courbe C lorsque le point M coïncide avec A. Ce critère s'applique parfaitement aux courbes algébriques pour lesquelles les coordonnées du point de contact seront des racines doubles des équations donnant les points d'intersection. L'initiateur de ces méthodes n'est autre que René Descartes.

Le plus célèbre des philosophes français est né en 1596 à La Haye en Touraine dans une famille de petite noblesse. Après des études de droit et de médecine achevées en 1616, il partage les neuf années suivantes entre des voyages, des engagements dans diverses armées et des temps d'étude. En 1628 il s'installe en Hollande et y rédige son œuvre, tout en correspondant avec les savants européens. Il quitte la Hollande en 1649 pour la cour de la reine Christine de Suède et meurt à Stockholm en 1650. En 1637 Descartes publie à Leyde son Discours de la Méthode, accompagné de trois traités scientifiques : la Dioptrique, les Météores et la Géométrie.


La Géométrie rééd. 1695
Source : gallica.bnf.fr / BnF

La Géométrie est le seul livre de Descartes sur les mathématiques, (mais la correspondance de Descartes contient de nombreux travaux mathématiques). Son but est de montrer que l'on peut ramener la résolution des problèmes de géométrie à celle de quelques équations algébriques, ou selon les termes de l'auteur (voir note 1) :

Ainsi, voulant résoudre quelque problème, on doit d'abord le considérer comme déjà fait, et donner des noms à toutes les lignes qui semblent nécessaires pour le construire, aussi bien à celles qui sont inconnues qu'aux autres. Puis, sans considérer aucune différence entre ces lignes connues et inconnues, on doit parcourir la difficulté selon l'ordre qui montre le plus naturellement de tous en quelle sorte elles dépendent mutuellement les unes des autres, jusques à ce qu'on ait trouvé moyen d'exprimer une même quantité en deux façons, ce qui se nomme une équation . ([DESb], p.3)

Les notations simplifiées utilisées par Descartes sont très proches des nôtres et nous rendent familière sa Géométrie. Cependant on n'y trouve pas de manière explicite des couples de coordonnées ou la donnée d'un repère « cartésien ». Il faut également noter que Fermat a développé à la même époque une géométrie analytique voisine de celle de Descartes. Et bien des siècles auparavant, les mathématiciens arabes avaient jeté des ponts entre l'algèbre et la géométrie : en particulier Omar Al Khayyâm au 11e siècle lorsqu'il avait montré que la résolution de n'importe quelle équation cubique se ramenait à la recherche des points d'intersection de deux coniques (cf. biblio).

Il est important de souligner que Descartes ne retient dans la Géométrie que les courbes susceptibles d'avoir une équation polynomiale, les autres, comme la quadratrice ou la spirale , qualifiées de courbes mécaniques, en sont exclues. On trouve également dans le livre III de la Géométrie un exposé des connaissances de Descartes en théorie des équations : en particulier « qu'en chaque équation, autant que la quantité inconnue a de dimensions, autant peut-il y avoir de diverses racines », que les racines peuvent être vraies ou fausses (i.e.positives ou négatives), ou quelquefois seulement imaginaires, qu'un nombre a est racine d'une équation polynomiale si et seulement si le polynôme en question est divisible par le binôme x - a. Y est également énoncée la règle pour déterminer le nombre de vraies ou de fausses racines d'une équation.

Descartes expose sa méthode des tangentes dans le livre II de la Géométrie. En fait il cherche à déterminer la normale à une courbe, ou plus précisément la sous normale c'est-à-dire la distance entre le point origine et le point d'intersection de la normale avec le premier axe. Pour ce faire il envisage un cercle passant par un point fixe C de la courbe donnée et dont le centre P appartient à ce premier axe ; ce cercle sera tangent à la courbe au point C si et seulement si la droite CP est la normale à la courbe (figure 1). Descartes commence par rechercher les équations que doivent vérifier les coordonnées des points d'intersection de la courbe et du cercle, puis va donner une condition pour qu'une de ces équations polynomiales aient une racine double e : à savoir que le polynôme soit divisible par (y - e)2 si la variable est y. Ce qui lui permettra de déterminer e par identification des coefficients du polynôme.


Figure 1

Voici un premier extrait dans lequel Descartes établit l'équation du cercle de centre P passant par C puis en tire deux formules de substitution. En termes modernes il utilise un repère orthogonal d'origine A dont un des axes est la droite AG et on notera que les paramètres v et s qu'il introduit (abscisse du point P et rayon de cercle ne sont pas indépendants.

Façon générale pour trouver des lignes droites, qui coupent les courbes données ou leurs contingentes, à angles droits.
Soit CE la ligne courbe [figure 1], et qu'il faille tirer une ligne droite par le point C, qui fasse avec elle des angles droits. Je suppose la chose déjà faite, et que la ligne cherchée est CP, laquelle je prolonge jusqu'au point P, où elle rencontre la ligne droite GA, que je suppose être celle aux points de laquelle on rapporte tous ceux de la ligne CE ; en sorte que faisant MA ou CB = y, et CM ou BA = x, j'ai quelque équation qui explique le rapport qui est entre x et y ; puis je fais PC = s, et PA = v, ou PM = v - y ; et à cause du triangle rectangle PMC, j'ai ss, qui est le carré de la base, égal à xx + vv - 2vy + yy, qui sont les carrés des deux côtés ; c'est à dire j'ai x = √ss - vv +2vy - yy ou bien y = v + √ss - xx, et par le moyen de cette équation, j'ôte de l'autre équation, qui m'explique le rapport qu'ont tous les points de la courbe CE à ceux de la droite GA, l'une des deux quantités indéterminées x ou y ; ce qui est aisé à faire en mettant partout √ss - vv +2vy - yy au lieu de x, et le carré de cette somme au lieu d'xx, et son cube au lieu d' x3, et ainsi des autres, si c'est x que je veuille ôter ; ou bien si c'est y, en mettant en son lieu v + √ss - xx et le carré, ou le cube, etc. de cette somme, au lieu d'yy, ou y3 etc. De façon qu'il reste toujours après cela une équation, en laquelle il n'y a plus qu'une seule quantité indéterminée, x, ou y. ([DESa], p.413-414)

Descartes applique sa méthode sur trois exemples. Nous ne présentons ici que le premier (une ellipse passant par A de grand axe q et de petit axe r).


Figure 2

Comme si CE est une ellipse [figure 2], et que MA soit le segment de son diamètre, auquel CM soit appliquée par ordre, et qui ait r pour son côté droit, et q pour le traversant, on a par le 13e th. du 1er liv. d'Apollonius,
xx = ry -  r  yy.
q
d'où ôtant xx, il reste ss - vv + 2vy - yy = ry -  r  yy.
q
Ou bien,  yy +  qry - 2qvy + qvv - qss   égal à rien.
q-r
car il est mieux en cet endroit de considérer ainsi ensemble toute la somme, que d'en faire une partie égale à l'autre.  ([DESa], p.414-415)

Dans ce second extrait Descartes explique de façon très détaillée le critère de contact par coïncidence de deux points d'intersection.

Or après qu'on a trouvé une telle équation, au lieu de s'en servir pour connaître les quantités x, ou y, ou z, qui sont déjà données, puisque le point C est donné, on la doit employer à trouver v, ou s, qui déterminent le point P, qui est demandé. Et à cet effet il faut considérer, que si ce point P est tel qu'on le désire, le cercle dont il sera le centre, et qui passera par le point C, y touchera la ligne courbe CE, sans la couper : mais que si ce point P, est tant soit peu plus proche, ou plus éloigné du point A, qu'il ne doit, ce cercle coupera la courbe, non seulement au point C, mais aussi nécessairement en quelque autre. Puis il faut aussi considérer, que lorsque ce cercle coupe la ligne courbe CE, l'équation par laquelle on cherche la quantité x, ou y, ou quelque autre semblable, en supposant PA et PC être connues, contient nécessairement deux racines, qui sont inégales. Car par exemple si ce cercle coupe la courbe aux points C et E [figure 3], ayant tiré EQ parallèle à CM, les noms des quantités indéterminées x et y, conviendront aussi bien aux lignes EQ, et QA, qu'à CM, et MA ; puis PE est égale à PC, à cause du cercle, si bien que cherchant les lignes EQ et QA, par PE et PA qu'on suppose comme données, on aura la même équation, que si on cherchait CM et MA par PC, PA, d'où il suit évidemment, que la valeur d'x, ou d'y, ou de telle autre quantité qu'on aura supposée, sera double en cette équation, c'est à dire qu'il y aura deux racines inégales entre elles ; et dont l'une sera CM, l'autre EQ, si c'est x qu'on cherche ; ou bien l'une sera MA, et l'autre QA, si c'est y, et ainsi des autres. Il est vrai que si le point E ne se trouve pas du même côté de la courbe que le point C ; il n'y aura que l'une de ces deux racines qui soit vraie, et l'autre sera renversée, ou moindre que rien : mais plus ces deux points , C et E, sont proches l'un de l'autre, moins il y a de différence entre ces deux racines ; et enfin elles sont entièrement égales, s'ils sont tous deux joints en un ; c'est à dire si le cercle, qui passe par C, y touche la courbe CE sans la couper. ([DESa], p.417-418)


Figure 3

Puis il explicite la forme générale de prend l'équation aux abscisses (ou aux ordonnées) des points d'intersection lorsqu'elle comporte une racine double et indique comment trouver les valeurs correspondantes des paramètres v et s par identification avec un polynôme de la forme (x - e)2 Q(x) où Q est un polynôme quelconque de degré égal à celui de l'équation moins deux.

De plus il faut considérer, que lorsqu'il y a deux racines égales en une équation, elle a nécessairement la même forme, que si on multiplie par soi même la quantité qu'on y suppose être inconnue moins la quantité connue qui lui est égale, et qu'après cela si cette dernière somme n'a pas tant de dimensions que la précédente, on la multiplie par une autre somme qui en ait autant qu'il lui en manque ; afin qu'il puisse y avoir séparément équation entre chacun des termes de l'autre. ([DESa], p.418-419)

Il ne reste plus qu'à illustrer la technique précédemment décrite en l'appliquant à des exemples comme celui de l'ellipse.

Comme par exemple je dis que la première équation trouvée ci-dessus,
à savoir,  yy +  qry - 2qvy + qvv - qss
q-r
doit avoir la même forme que celle qui se produit en faisant e égal à y, et multipliant y - e par soi-même, d'où il vient yy - 2ey + ee, en sorte qu'on peut comparer séparément chacun de leurs termes, et dire que puisque le premier qui est yy, est tout le même en l'une qu'en l'autre,
le second qui est en l'une    qry - 2qvy
q-r
est égal au second de l'autre qui est -2ey, d'où cherchant la quantité v qui est la ligne PA [figure 4],
on a   v = e -  r  e +  r
q 2
ou bien à cause que nous avons supposé e égal à y,
on a   v = y -  r  y +  r
q 2
Et ainsi on pourrait trouver s par le troisième terme mais pour ce que la quantité v détermine assez le point P, qui est le seul que nous cherchions, on n'a pas besoin de passer outre. ([DESa], p.419)


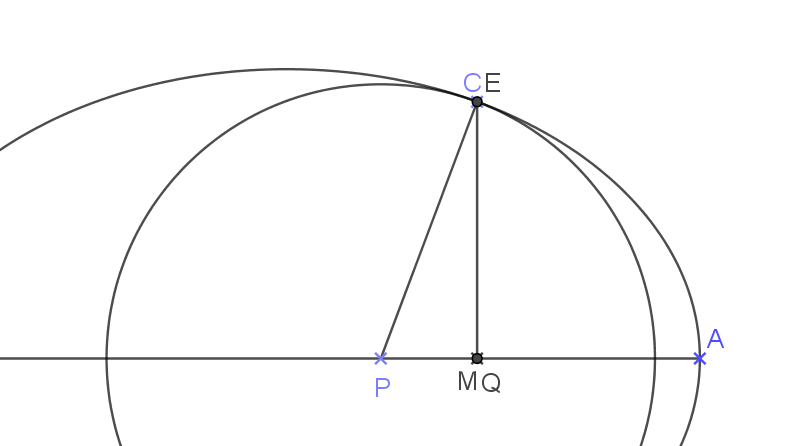Figure 4

Dans sa conclusion Descartes affirme (à juste titre) que sa méthode s'étend à toutes les courbes relevant de sa Géométrie :

C'est pourquoi composant la ligne AP, de cette somme égale à v dont toutes les quantités sont connues, et tirant du point P ainsi trouvé, une ligne droite vers C, elle y coupe la courbe CE à angles droits [figure 1], qui est ce qu'il fallait faire. Et je ne vois rien qui empêche, qu'on n'étende ce problème en même façon à toutes les lignes courbes, qui tombent sous quelque calcul géométrique.([DESa], p.422)
Notes
  1. L'orthographe de Descartes pouvant dérouter le lecteur d'aujourd'hui nous l'avons modernisé ; en revanche pour les expressions mathématiques nous avons conservé les notations de Descartes, à une exception près le signe d'égalité que Descartes note . (Retour au texte)
Bibliographie

    Autres ouvrages

  1. Bourbaki Nicolas Eléments d'histoire des mathématiques. Masson, Paris, 1984.
  2. Collette Jean-Paul Histoire des mathématiques tome 2. Editions du Renouveau Pédagogique Inc., Montréal, 1973. Diff. Vuibert, Paris
  3. I.R.E.M. Groupe Epistémologie et Histoire. Mathématiques au fil des âges. Gauthier-Villars, Paris, 1987.
  4. Rashed R. & Vahabzadeh B. Al-Khayyâm mathématicien. Albert Blanchard, Paris, 1999.

Chapitre suivant


Image de fond : source gallica.bnf.fr/BnF