Courbes et tangentes au 17^e siècle

Chapitre 3 : La méthode de Fermat

Peu de temps après la publication de la Méthode de M. Descartes pour les tangentes, M. de Fermat en trouva aussi une, que M. Descartes a enfin avoué lui-même être plus simple en bien des rencontres que la sienne.
Guillaume De L'Hospital : préface de l'Analyse des infiniment petits

Parallèlement aux travaux décrits dans les deux précédents chapitres d'autres méthodes vont voir le jour. Exploitant la nouvelle géométrie de Fermat et de Descartes, elles consistent en un calcul opérant sur l'équation de la courbe (voir note 1) et se caractérisent par l'utilisation de quantités infiniment petites. La tangente dont l'existence est supposée à priori possède toutes les propriétés géométriques déjà connues, plus celle de se confondre avec la courbe au voisinage du point de contact. Ces nouvelles méthodes analytiques, dont les plus remarquables sont celles de Fermat et de Barrow, vont se révéler plus générales que les précédentes et donneront naissance au calcul différentiel.

Pierre de Fermat

Né à Beaumont de Lomagne en 1601, fils d'un commerçant fortuné, Fermat fit carrière dans la magistrature de Toulouse et de Castres. Il pratiquait les mathématiques à ses moments de loisir et ne prenait pas la peine de publier ses découvertes, se contentant de les communiquer à un correspondant. Souvent il ne donnait que le principe général de ses démonstrations sans entrer dans les détails. Ce qui ne l'empêcha pas d'acquérir une immense réputation dans le milieu savant de son époque. Son fils Samuel se chargea d'éditer les travaux mathématiques de son père après sa mort en 1665.
On oublie souvent que Descartes doit partager avec Pierre de Fermat l'invention de la géométrie analytique puisque celui-ci en avait énoncé les principes dans un mémoire de 1636. Fermat développa des méthodes de calcul des tangentes et de quadrature qui en font un précurseur du calcul différentiel et intégral. Sa correspondance avec Pascal en 1654 sur la résolution de quelques problèmes de jeux de hasard fait de lui le cofondateur du calcul des probabilités. Mais la part la plus grande de sa célébrité provient de ses remarquables travaux en théorie des nombres : méthode de la descente infinie, « petit théorème de Fermat » et bien sur l'énoncé du « grand théorème » qui devait fasciner des générations de mathématiciens avant d'être finalement démontré en 1993 par Andrew Wiles. Enfin n'oublions pas sa contribution à l'optique lorsqu'il démontre en 1661 que les lois de la réfraction de Descartes peuvent se déduire du principe naturel suivant lequel la lumière suit toujours le plus court chemin (en temps).

La méthode pour la recherche du maximum et du minimum

Dès 1629 Fermat est en possession de sa règle pour la détermination des extrema d’une fonction qu’il applique en particulier au problème des tangentes. Il la fait connaître au début de l’année 1638 en réaction à la méthode préconisée par Descartes dans sa Géométrie. Par la suite il rédigera cinq autres textes consacrés à sa méthode dans lesquels il donne de nouvelles applications et essaie d’en préciser les principes. Tous ces écrits ont été rassemblés par son fils Samuel dans les Varia Operia et traduits du latin par Paul Tannery et Charles Henry. Nous allons tenter d’analyser la méthode de Fermat, exercice difficile pour un lecteur moderne toujours à la merci de tomber dans la surinterprétation.

La Méthodus ad disquirendam maximam et minimam se présente comme un algorithme portant sur l’expression algébrique de la quantité variable dont on cherche l’extremum. Cet algorithme conduit à une équation dont la solution fournit l’abscisse de l’extremum. Dans ce premier écrit Fermat ne fournit pas d’explications sur les principes de sa méthode. Enfin il faut signaler que Fermat avait conservé les notations de Viète, bien plus lourdes que celles de Descartes (voir note 2):

Toute la théorie de la recherche du maximum et du minimum suppose la position de deux inconnues et la seule règle que voici :
Soit a une inconnue quelconque de la question (qu'elle ait une, deux ou trois dimensions, suivant qu'il convient d'après l'énoncé). On exprimera la quantité maxima ou minima en a, au moyen de termes qui pourront être de degrés quelconques. On substituera ensuite a + e à l'inconnue primitive a, et on exprimera ainsi la quantité maxima ou minima en termes où entreront a et e à des degrés quelconques. On adégalera [littéralement rendra égal], pour parler comme Diophante, les deux expressions de la quantité maxima ou minima, et on retranchera les termes communs de part et d'autre. Cela fait, il se trouvera que de part et d'autre tous les termes seront affectés de e ou d'une de ses puissances. On divisera tous les termes par e, ou par une puissance de e d'un degré plus élevé, de façon que dans l'un au moins des termes de l'un quelconque des membres e disparaisse entièrement. On supprimera ensuite tous les termes où entrera encore e ou l'une de ses puissances et l'on égalera les autres, ou bien, si dans l'un des membres il ne reste rien, on égalera, ce qui revient au même, les termes en plus aux termes en moins. La résolution de cette dernière équation donnera la valeur de a, qui conduira au maximum ou au minimum, en reprenant sa première expression.
Voici un exemple :
Soit à partager la droite AC en E (figure 1), en sorte que AE × EC soit maximum.
Notons b le segment AC ; soit a un des segments, l'autre sera b - a, et le produit dont on doit trouver le maximum : ba - a². Soit maintenant a + e le premier segment de b, le second sera b - a - e, et le produit des segments : ba - a² + be - 2ae - e²;
Il doit être adégalé au précédent : ba - a² ;
Supprimant les termes communs : be sera adégalé à 2ae + e² ;
Divisant tous les termes : b sera adégalé à 2a + e ;
Supprimez e : b sera égal à 2a.
Pour résoudre le problème il faut donc prendre la moitié de b. Il est impossible de donner une méthode plus générale. » ([FER], t.3, p121-123)

A           E                   C

Figure 1

Fermat a donc adégalé les expressions ba – a² (que nous noterons f(a) ) et ba – a² + be - 2ae – e² ( = f(a + e) ). Comment devons nous comprendre ce terme ? L’auteur fournit quelques explications dans son troisième écrit consacré à sa méthode à propos du maximum de l’expression : a²b – a³ .

Prenons maintenant a + e au lieu de a, on aura pour le solide (a + e)² (b – a - e) […] .
Je le compare au premier solide : a²b – a³ , comme s’ils étaient égaux quoiqu’en fait ils ne le soient point. C’est cette comparaison que j’appelle adégalité, pour parler comme Diophante, car on peut ainsi traduire le mot grec παρισοτης dont il se sert. ([FER], t.3, p126)

Ces précisions nous permettent de proposer une première interprétation du terme « adégaler ». Le substantif παρισοτης est dérivé de l’adjectif παρισος qui signifie presque égal. Fermat le traduit en latin par adaequalitas formé à partir du verbe adaequare qui a pour sens premier « rendre égal » et s’emploie aussi dans le sens de « comparer, assimiler ». Ces considérations étymologiques mènent à deux significations possibles du verbe adégaler : « considérer comme égales » et « être presque égal ». Nous allons voir par la suite que Fermat joue avec les deux.

Une autre question surgit immédiatement : comment Fermat sait-il que cette méthode conduit toujours à un extremum ? Cette fois c’est dans son quatrième opuscule consacré à cette méthode du maximum et du minimum que Fermat, poussé par les critiques de ses contemporains, donne quelques éléments de réponses. Nous allons essayer de résumer ses propos. Fermat dit que sa méthode lui « est venu à l’esprit » en étudiant une méthode de Viète qui permet de trouver une relation entre deux racines d’une même équation polynomiale. La démarche est la suivante : soit a et e deux racines distinctes de l’équation P(x) = k . Des deux « équations corrélatives » P(a) = k et P(e) = k, on déduit immédiatement la relation P(a) – P(e) = 0 ; il est clair que l’expression P(a) – P(e) est divisible par (a – e), par conséquent on obtient en effectuant cette division une relation que vérifie nécessairement le couple (a , e). Soit Q (a , e) = 0 cette relation.

Supposons maintenant que P ne prenne que des valeurs positives (c’est le cas des trois exemples traités par Fermat qui sont des problèmes d’origine géométrique du type partager un segment de façon que tel produit soit maximum ou tel rapport soit minimum). Pour fixer les idées disons que P est un produit dont la valeur maximale est M. La relation précédente est bien sur valable pour tout k tel que 0 < k < M et Fermat fait remarquer que les points a et e « se trouveront situés de part et d’autre du point correspondant au produit maximum » et que plus k augmentera « plus au contraire diminuera la différence entre a et e, jusqu’à ce qu’elle s’évanouisse tout à fait pour la division [le partage du segment] correspondant au produit maximum ; dans ce cas il n’y a qu’une solution unique et singulière, les deux quantités a et e devenant égales ». C’est pourquoi selon Fermat si l’on fait a = e dans la relation Q (a , e) = 0 on obtiendra la relation que doit vérifier l’abscisse du maximum.

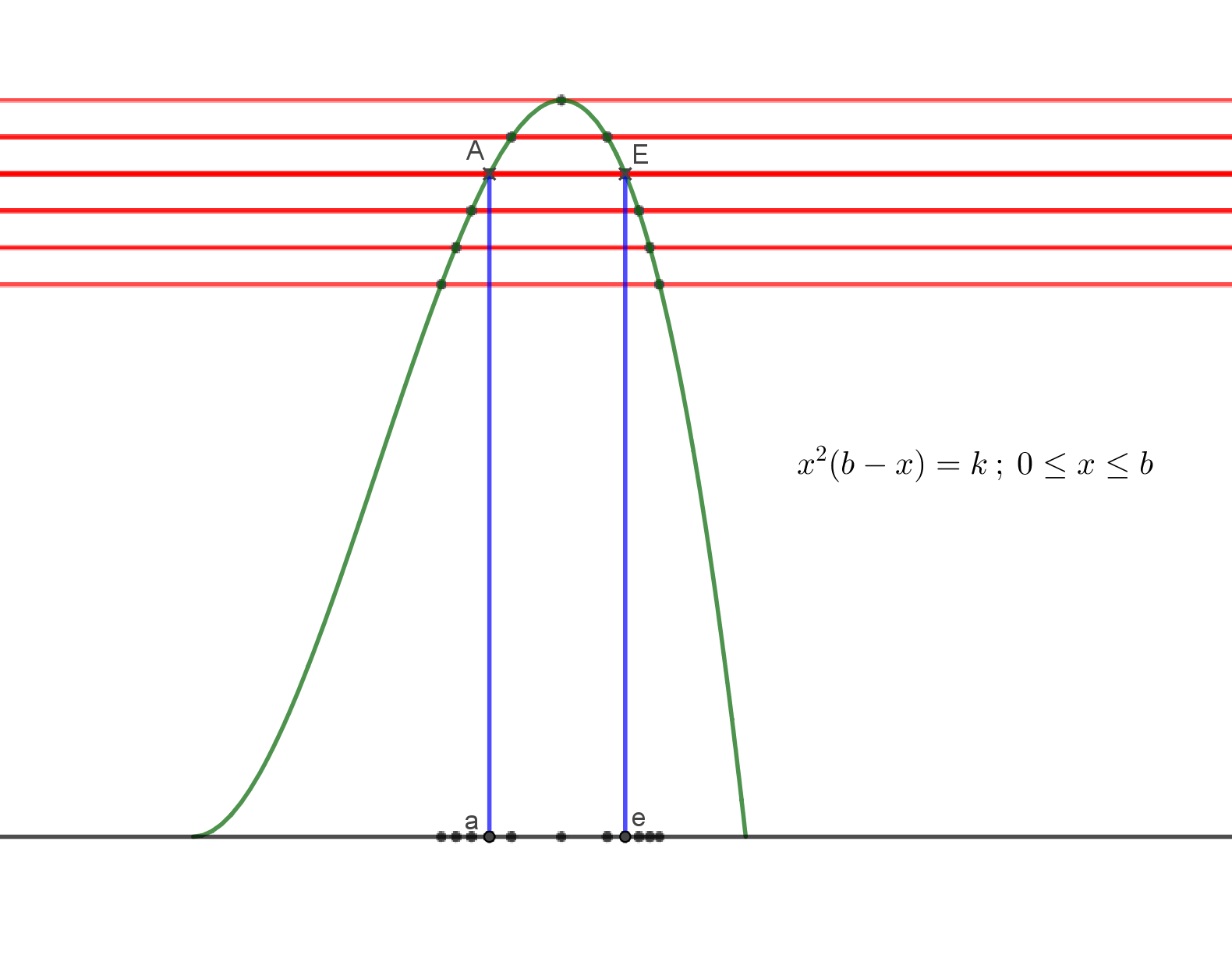
Figure 2

Voici le détail des calculs concernant le deuxième exemple proposé par Fermat :
Soit à trouver le maximum de    a²b – a³ :
On pose donc :    a²b – a³ = e²b – e³
soit encore :    a²b – e²b = a³ – e³
Après division par a – e , il vient :   ab + eb = a² + ae + e²
Pour trouver la valeur donnant le maximum faisons a = e ; il vient :   2b = 3a.

Pour éviter les divisions par le binôme a – e qui peuvent être pénibles, Fermat propose un raffinement de la méthode consistant à prendre comme inconnues a et a + e au lieu de a et e. Dans ce cas e désignera la différence des deux racines de l’équation.
Les explications précédentes fournies par Fermat sur l’origine de sa méthode peuvent être vues comme étant de nature purement algébrique. En termes actuels elles reviendraient à dire que si la fonction rationnelle R admet au point a un extremum de valeur A alors l’équation R(x) = A admet a pour racine double. De ce point de vue il n’est pas besoin de considérer la différence des inconnues e comme une quantité infiniment petite. (voir note 3)
Mais nous allons voir que ces premières explications ne répondent pas à toutes les questions soulevées par l’application de sa méthode à la recherche des tangentes.

Le calcul de la tangente à la parabole

Regardons maintenant comment Fermat utilise sa méthode d'adégalisation pour déterminer les tangentes.

Nous ramenons à la méthode précédente l'invention des tangentes en des points donnés à des courbes quelconques. Soit donnée, par exemple, la parabole BDN [figure 3], de sommet D, de diamètre DC ; soit donné sur elle le point B, par lequel il faut mener la droite BE tangente à la parabole et rencontrant le diamètre en E. Si l'on prend sur la droite BE un point quelconque O, dont on mène l'ordonnée OI, en même temps que l'ordonnée BC du point B, on aura :

CD >   BC²

DI OI²

puisque le point O est extérieur à la parabole. Mais

BC² =   CE²

OI² IE²

à cause de la similitude des triangles. Donc

CD >   CE²

DI IE²

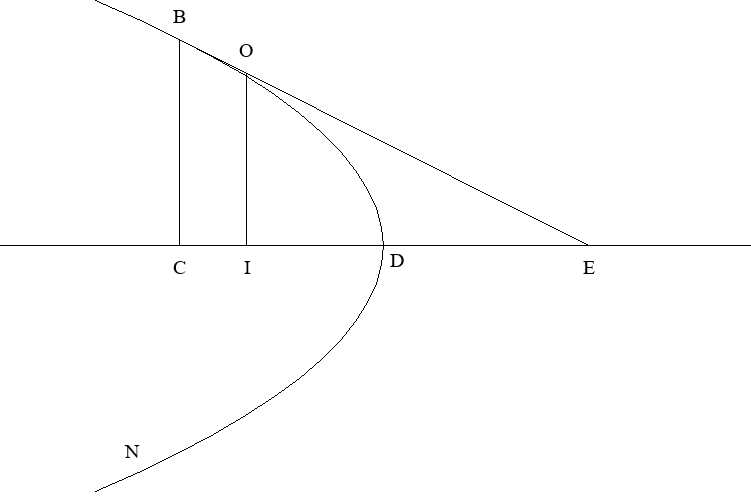
Figure 3

Fermat étant, comme de coutume, plutôt avare d'explications quelques précisions sont nécessaires avant d'aborder la suite. La courbe étudiée est une parabole d'équation y² = kx ; soit avec les notations de Fermat BC² = kCD. Fermat remarque que si un point O appartient à la tangente en B à la parabole, alors

OI²	≥	BC²
ID	≥	CD

l'égalité n'ayant lieu que lorsque O est en B. Cette inégalité peut se justifier par des propriétés de convexité, la demi parabole DB étant toujours située sous ses tangentes ; remarquons que ce sont ces mêmes propriétés de convexité qu’utilisait déjà Apollonius pour déterminer la tangente à la parabole.
Il en résulte immédiatement que lorsque le point I décrit la demi-droite EC (O décrivant la tangente EB) le rapport ^OI²⁄_ID admet un minimum lorsque I est confondu avec C.
On peut donc en adégalant les deux expressions ^OI²⁄_ID et ^BC²⁄_CD, déterminer la position du point C sur la demi-droite ED.
Revenons maintenant au texte de Fermat.

Or le point B est donné, donc l'ordonnée BC, donc le point C, donc CD. Soit donc CD = d, donnée. Posons CE = a et CI = e ; on aura .

d >   a²

d - e a² + e² - 2ae

Faisons le produit des moyens et des extrêmes :
da² + de² - 2dae > da² - a²e.
Adégalons donc, d'après la méthode précédente ; on aura, en retranchant les termes communs :
de² - 2dae     sera adégalé à     - a²e,
ou, ce qui revient au même :
de² + a²e     sera adégalé à     2dae.
Divisez tous les termes par e :
de + a²     sera adégalé à     2 da.
Supprimez de : il reste a² = 2da, donc : a = 2d.
Nous prouvons ainsi que CE est double de CD, ce qui est conforme à la vérité.
Cette méthode ne trompe jamais, et peut s'étendre à nombre de questions très belles ; grâce à elle, nous avons trouvé les centres de gravité de figures terminées par des lignes droites et courbes, aussi bien que ceux de solides et nombre d'autres choses dont nous pourrons traiter ailleurs, si nous en avons le loisir. (voir note 4) ([FER], t.3, p121-123)

Une animation pour voir les variations du rapport OI²/ID : Montrer

Il faut bien reconnaître que Fermat ne facilite pas le travail du lecteur qui veut comprendre en quoi la détermination de la tangente à une courbe se ramène à une recherche d’extremum, car il n’indique pas explicitement la quantité variable qui admet un minimum. Ceci peut laisser croire à ses contemporains qu’il ne maîtrise pas les fondements de sa méthode (voir ci-après la critique de Descartes) et que sa seule justification est de retrouver les résultats connus des anciens géomètres.

Si l’on examine les autres exemples de calcul de tangentes présents dans l’ensemble des textes de Fermat consacré à sa méthode des maxima et minima, on constate que l’inégalité de convexité n’est présente que dans le calcul de la tangente à l’ellipse figurant dans le troisième opuscule ; pour les autres exemples qui figurent tous dans le sixième texte Fermat va reformuler sa description de la méthode. Voici ce qu’il en dit dans le cas d’une courbe définie en termes de distances par rapport à deux droites données :

Nous considérons en fait dans le plan d’une courbe quelconque deux droites de position, dont on peut appeler l’une diamètre, l’autre ordonnée. Nous supposons la tangente déjà trouvée en un point donné de la courbe, et nous considérons par adégalité la propriété spécifique de la courbe, non plus sur la courbe elle-même, mais sur la tangente à trouver. En éliminant suivant notre théorie des maxima et minima, le termes qui doivent l’être, nous arrivons à une égalité qui détermine le point de rencontre de la tangente avec le diamètre, par suite la tangente elle-même.

Ainsi qu’on pourra le vérifier dans l’exemple qui suit « considérer par adégalité la propriété spécifique de la courbe, non plus sur la courbe elle-même, mais sur la tangente » revient à confondre la courbe avec sa tangente au voisinage du point de contact.

Aux nombreux exemples que j’ai déjà données, j’ajouterai celui de la tangente à la cissoïde, inventée, dit-on, par Dioclès. Soient un cercle dont les deux diamètres AG, BI [figure 4] se coupent normalement, et la cissoïde IHG, à laquelle, par un quelconque de ses points, soit H, il faut mener la tangente.

Figure 4

Supposons le problème résolu, et F l’intersection de CG et de la tangente HF. Posons DF = a, et, en prenant un point E quelconque entre D et F, DE = e.
D’après la propriété spécifique de la cissoïde : ^MD⁄_DG = ^DG⁄_DH    on aura donc à exprimer analytiquement l’adégalité entre ^NE⁄_EG et ^EG⁄_EO    EO étant la portion de la droite EN interceptée entre E et la tangente.
Soient la donnée AD = z, la donnée DG = n, la donnée DH = r, et, comme nous l’avons dit, l’inconnue DF = a, l’arbitraire DE = e.
On aura

EG = a – e ,  EO = ar - er ,  EN = √zn - ze + ne - e²

a

D’après la règle, il faut considérer la propriété spécifique, non pas sur la courbe, mais sur la tangente, et poser donc ^NE⁄_EG = ^EG⁄_EO   EO étant l’ordonnée de la tangente.[…]

L’expression analytique de EO exprime le fait que O appartient à la tangente et l’adégalité entre ^NE⁄_EG et ^EG⁄_EO revient à dire que O appartient à la cissoïde. Par conséquent l’arbitraire e peut dans ce cas être interprété comme un infiniment petit.

Ces différents extraits nous permettent de mieux comprendre comment Fermat est parvenu à sa méthode des tangentes. Partant d’une technique de calcul algébrique permettant de trouver un extremum d’une fonction rationnelle et après avoir ramené la détermination des tangentes à la recherche d’un extremum d’une certaine quantité, il finit par exhiber ce qui est au cœur de son algorithme : exprimer qu’un point de la tangente infiniment voisin du point de contact vérifie aussi l’équation de la courbe.

Notes

Le concept de fonction ne sera dégagé qu'au siècle suivant. Si par la suite nous utilisons ce terme anachronique, ce n'est que pour faciliter la compréhension du lecteur moderne. (Retour au texte)
Fermat note : B in A – Aq. + B in E – A in E bis – Eq. l'expression : ba - a² + be - 2ae - e² (Retour au texte)
L'utilisation de cet algorithme dans le cas d'un polynôme ne nécessite pas de poser que e est un infiniment petit. Mais la preuve de la validité de cet algorithme repose bien sur un argument de continuité (lorsque Fermat affirme que la relation Q(a, a+e) = 0 reste vraie pour e = 0). Le diable se cache dans les détails ! (Retour au texte)
On trouve dans les Operia Varia édité par son fils Samuel, le calcul des tangentes à l'ellipse, à la cissoïde, à la conchoïde, à la cycloïde et à la quadratrice. Fermat y signale également que sa méthode permet de déterminer un point d'inflexion d'une courbe, puisque en un tel point l'expression qui exprime l'inclinaison de la tangente sur l'axe des abscisses est à l'état de maximum ou de minimum. (Retour au texte)

Bibliographie

Textes originaux cités

[FER] Fermat Pierre de. Œuvres, éd. P. Tannery. Paris, Gauthier-Villars, 1891-1922.

Autres ouvrages

Barbin Evelyne La révolution mathématique du XVII^e siècle. Ellipses, Paris 2006.
Bourbaki Nicolas Eléments d'histoire des mathématiques. Masson, Paris, 1984.
Brassine E. Précis des œuvres mathématiques de P. Fermat. Imprimerie J-M. Douladoure, Toulouse, 1853.
Collette Jean-Paul Histoire des mathématiques tome 2. Editions du Renouveau Pédagogique Inc., Montréal, 1973. Diff. Vuibert, Paris
I.R.E.M. Groupe Epistémologie et Histoire. Mathématiques au fil des Âges. Gauthier-Villars, Paris, 1987.

Courbes et tangentes au 17e siècle