Courbes et tangentes au 17e siècle
Chapitre 1 : La méthode de Roberval
Il peut arriver aussi qu'une courbe soit donnée par la loi du mouvement d'un point
générateur ; et alors, pour lui mener une tangente, si l'on ne veut pas avoir recours
à l'analyse, on peut employer la méthode de Roberval. Cette méthode, qu'il inventa
avant que Descartes eût appliqué l'algèbre à la géométrie, est implicitement comprise
dans les procédés du calcul différentiel, et c'est pour cela que les éléments de
mathématiques n'en font pas mention.
Gaspard Monge : Leçons à l'Ecole normale
Il faut attendre le 17e siècle pour que, dans les travaux des précurseurs du calcul infinitésimal, le problème des tangentes soit abordé d'un point de vue radicalement différent. Le développement de ce nouveau calcul est la réponse à trois problématiques intimement liées : définir rigoureusement les concepts cinématiques (vitesse instantanée, accélération), étudier les propriétés des lignes courbes (tangentes, courbure, rectification, quadrature, centre de gravité), traduire mathématiquement les lois de la nature.
A l'origine se trouvent les travaux de Kepler et Galilée. Le premier, en énonçant ses lois sur les trajectoires elliptiques des planètes, et le second, en posant les bases de la mécanique, orientent les travaux des mathématiciens vers l'étude des courbes considérées comme trajectoires d'un point en mouvement et plus généralement vers la mathématisation des lois qui régissent l'Univers. Galilée a montré la voie à suivre en écrivant en 1623 dans Il Saggiatore à propos de la langue qu'il faut apprendre pour pouvoir lire le vaste livre qu'est l'Univers : elle est écrite en langue mathématique et ses lettres sont des triangles, des cercles et d'autres figures géométriques, moyens sans lesquels il est humainement impossible de comprendre un seul mot.
Dans le second quart du 17e siècle vont éclore nombre de méthodes originales de détermination de la tangente. Il est possible, avec le recul du temps, de les classer en trois catégories selon qu'elles relèvent davantage de la cinématique, de l'algèbre ou du calcul infinitésimal proprement dit. Dans les textes présentés ci-après le lecteur pourra vérifier que les géomètres de ce siècle se sont libérés de la contrainte de rigueur de l'exposé héritée des mathématiques grecques et nous donnent à voir le résultat de leurs travaux de recherche avec les imprécisions et les imperfections d'une science naissante.
Soulignons également la mauvaise organisation du monde scientifique avant la création des sociétés savantes (voir note 1). Les auteurs ne pouvaient faire connaître leurs travaux qu'à travers des échanges épistolaires ou en faisant imprimer des livres fort coûteux lorsqu'ils trouvaient un riche mécène. Si on ajoute à cela le fait que les adversaires étaient prompts à déclencher des controverses, on comprend mieux pourquoi, sur un sujet aux principes aussi incertains que le calcul différentiel, nombre de savants de ce temps rechignaient à publier au grand jour leurs résultats. De telles conditions étaient également favorables à l'apparition de querelles de priorité entre des géomètres qui avaient travaillé sur le même sujet sans le savoir. Fort heureusement, certains amateurs de sciences, tel Mersenne à Paris qui était en relation avec de nombreux savants, permettaient une communication partielle des nouvelles méthodes.(voir note 2)
Les méthodes cinématiques
Elles reposent sur deux principes. Le premier est que la tangente à une courbe donne la direction « instantanée » du mouvement du point décrivant la courbe (c'est-à-dire la direction que prendrait à cet instant le point mobile s'il n'était plus forcé à suivre la courbe). C'est un fait d'expérience qui pouvait être facilement constaté avec une fronde ou une catapulte. Le second est le principe de composition des mouvements qui peut s'énoncer ainsi en termes actuels : le mouvement résultant de la composition d'un mouvement de vecteur vitesse u et d'un mouvement de vecteur vitesse v a pour vecteur vitesse w = u + v (cf. fig1). (On ne parlait évidemment pas de vecteur vitesse à cette époque).

Statue de Giordano Bruno,Campo dei fiori, Rome
Ce principe est déjà évoqué par Giordano Bruno (1548-1600), philosophe italien qui fut brûlé vif sur ordre du Saint Office en raison de ces opinions religieuses et politiques. Pour réfuter l'objection d'Aristote contre le mouvement de la Terre (si la Terre n'était pas immobile, une pierre lancée verticalement retomberait à l'ouest) Giordano Bruno imaginait l'expérience suivante : si deux hommes, l'un sur un navire en marche, l'autre sur la rive, laissent tomber simultanément du même endroit une pierre sur le pont du navire, alors la pierre lancée par l'homme sur la rive tombera en arrière car la pierre de l'homme porté par le navire se meut du mouvement même de ce navire ; elle a donc une certaine force imprimée que ne possède pas l'autre pierre.(Cena de le Ceneri (1584), cité in Histoire de la Mécanique, p.103).
C'est Galilée qui le premier énonce clairement le principe de composition des mouvements dans le cas particulier d'un projectile lancé dans le champ de pesanteur avec une direction initiale horizontale. Ecoutons le dans les discours sur deux sciences nouvelles (1638) :
J'imagine qu'un mobile a été lancé sur un plan horizontal d'où l'on a écarté tout obstacle ; il est déjà certain, d'après ce qu'on a dit ailleurs plus longuement, que son mouvement se poursuivra uniformément et éternellement sur ce même plan, pourvu qu'on le prolonge à l'infini. Supposons en revanche qu'il soit limité et situé à une certaine hauteur : le mobile que j'imagine doué de gravité, parvenu à l'extrémité du plan et continuant sa course, ajoutera à son précédent mouvement uniforme et indélébile la tendance vers le bas que lui confère sa gravité : le résultat sera ce mouvement composé d'un mouvement horizontal uniforme et d'un mouvement naturellement accéléré vers le bas... ([GAL], p.205).
Puis Galilée démontre qu'un projectile qu'entraîne un mouvement composé d'un mouvement horizontal uniforme et d'un mouvement naturellement accéléré vers le bas, décrit au cours de son déplacement une trajectoire semi parabolique (ibid.). Pour cela il explique qu'en des temps égaux le projectile parcourt dans la direction horizontale des espaces égaux auxquels s'ajoutent dans la direction verticale, conformément à sa loi des mouvements naturellement accélérés, des espaces qui sont comme les carrés des temps.
Le Français Roberval et l'Italien Torricelli vont développer chacun de leur côté une méthode originale de construction de la tangente reposant sur le principe de composition des mouvements. Roberval élabore sa méthode entre 1634 et 1637, mais elle ne sera publiée qu'en 1693 dans les mémoires de l'Académie Royale des Sciences. Torricelli, collaborateur de Galilée célèbre pour avoir mis en évidence la pression atmosphérique, expose sa méthode des tangentes en 1644 (voir note 3). Leurs méthodes s'inspirant des mêmes principes, il s'ensuivra une querelle de priorité entre les deux savants.
Les méthodes de Roberval et de Torricelli sont très efficaces lorsque la courbe est susceptible d'une définition cinématique simple.
Le calcul des tangentes chez Gilles Personne de Roberval

Première page du Traité de RobervalSource : gallica.bnf.fr / BnF
Gilles Personne vit le jour en 1602 dans une famille paysanne à Roberval, près de Senlis. En 1628 il s'établit à Paris et prend le nom de son lieu de naissance. Il entre en contact avec le Père Mersenne, qui restera un ami fidèle. En 1634 il obtient la chaire créée par Ramus au Collège Royal de France et la gardera jusqu'à sa mort en 1675 à Paris. Cette chaire était attribuée pour trois ans par concours, pour garder un avantage sur ses concurrents Roberval retardait la parution de ses travaux. Surtout connu du grand public pour la description de sa célèbre balance, Roberval a très peu publié de son vivant, un traité de statique en 1636 et un d'astronomie en 1644. En revanche il transmit à l'Académie des Sciences, dont il fut membre dès sa création en 1666, de nombreuses notes portant sur la cycloïde, la composition des mouvements, les quadratures par la méthode des indivisibles, la recherche des centres de gravité.
Les textes suivants sont extraits du traité publié en 1693 dans les mémoires de l'Académie des Sciences, qui s'intitule : Observations sur la composition des mouvements et sur le moyen de trouver les touchantes des lignes courbes. Considérant les courbes comme trajectoires d'un point mobile, Roberval y énonce les deux principes (ou règles) qui sous-tendent sa méthode des tangentes.
PROBLÈME I.
Proposition cinquième.
Donner les touchantes des lignes courbes par les mouvements mêmes mêlés.
Mais nous supposons qu'on nous en donne assez de propriétés spécifiques, qui nous fassent connaître les mouvements qui les décrivent.Axiome, ou principe d'invention.
La direction du mouvement d'un point qui décrit une ligne courbe, est la touchante de la ligne courbe en chaque position de ce point-là.
Le principe est assez intelligible, & on l'accordera facilement dès qu'on l'aura considéré avec un peu d'attention.Règle générale.
Par les propriétés spécifiques de la ligne courbe (qui vous seront données) examinez les divers mouvements qu'a le point qui la décrit à l'endroit où vous voulez mener la touchante : de tous ces mouvements composez en un seul, tirez la ligne de direction du mouvement composé, vous aurez la touchante de la ligne courbe.
([ROB], p.24-25)
La démonstration est mot à mot dans notre principe. Et parce qu'elle est très générale, & qu'elle peut servir à tous les exemples que nous en donnerons, il ne sera point à propos de la répéter.
Roberval applique ensuite sa méthode pour déterminer les tangentes aux coniques, à diverses conchoïdes, à la quadratrice, à la cissoïde, au limaçon de Pascal, à la spirale d'Archimède, à la cycloïde.
Le premier exemple est celui de la parabole. Roberval va utiliser comme description d'une parabole (dont le foyer et le sommet sont connus) celle qui résulte de la construction de la parabole point par point à la règle et au compas et dont l'équivalent moderne est « l'ensemble des points équidistants du foyer et de la directrice » (cf. fig.2).
Soit A le foyer, & F le sommet : soit tirée la ligne AF & prolongée de F vers B, & soit FB égale à AF la même ligne BFA sera l'axe de la parabole. Prenez dans FA autant de points I qu'il vous plaira, tirez par ces points des lignes perpendiculaires à FA ; du centre A & de l'intervale d'entre chaque perpendiculaire & le point B comme BI, décrivez des arcs de cercle dont chacun coupe une de ces perpendiculaires comme en E, la parabole passera par les points E. (ibid. p.25-26)
Roberval expose ensuite sa méthode de détermination de la touchante qui va s'appuyer sur la description précédente. La tangente apparait comme la diagonale d'un losange (le diamètre d'un rhombe pour Roberval) dont deux côtés sont parallèles à l'axe et les deux autres sont parallèles à la droite reliant le foyer au point courant.
Cela posé si l'on demande la touchante de la Parabole au point E, soit tiré la ligne AE prolongée comme en D, & la ligne EI perpendiculaire à AB, & encore la ligne HE parallèle à l'axe FAI, alors il est clair par la description ci-dessus, que le mouvement du point E décrivant la Parabole, est composé de deux mouvements droits égaux, dont l'un est la ligne AE, & l'autre est la ligne HE sur laquelle il se meut de même vitesse que le point I dans la ligne BA, laquelle vitesse est pareille à celle de la ligne AE par la construction, puisque AE est toujours égale à BI. Partant puisque la direction de ces mouvements égaux est connue, savoir suivant les lignes droites AED, HE données de position, si vous divisez l'angle AEH en deux également par la ligne LEC, qui est le diamètre d'un rhombe autour de l'angle AEH, (& par conséquent la direction du mouvement composé des deux HE AE,) la ligne LEC sera la touchante.
(ibid., p.26)
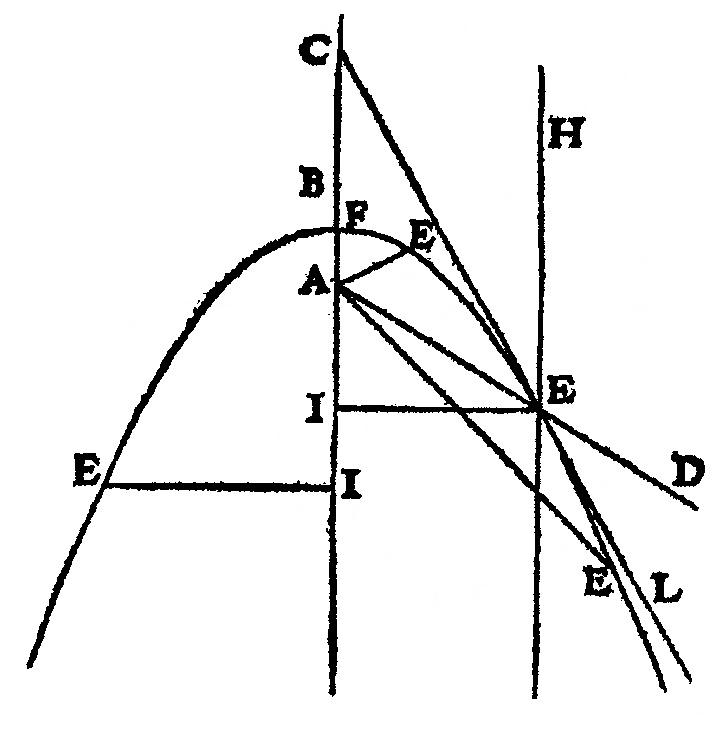
Fig.3 : reprod. planche du traité de Roberval
Source : gallica.bnf.fr / BnF
Il est facile de vérifier, comme Roberval se donne la peine de le faire, que sa façon de trouver les touchantes de la parabole, s'accorde avec celle d'Apollonius que nous avons rapportée dans l'article Courbes et tangentes dans les mathématiques grecques.
Le mouvement composé du point décrivant la parabole envisagé par Roberval relève plus d'une géométrie cinématique que de l'étude de la trajectoire d'un corps mobile. On peut cependant le rapprocher de la méthode usuelle pour tracer une parabole d'un mouvement continu à l'aide d'un fil et d'une équerre mobile (cf. animation), si on souhaite lui donner quelque réalité matérielle.
Traceur de parabole : Montrer l'animation
Le fil est fixé en A et en L. Sa longueur est égale à celle du côté HL de l'équerre. On maintient le crayon E sur le côté HL de façon que le fil soit tendu, tout en faisant glisser l'équerre le long de la règle d. Le point E décrit alors un arc de parabole de foyer A et de directrice d.
Roberval fait remarquer, à juste titre, que dans la description de la parabole qu'il a choisie le mouvement du point E n'est pas uniforme. Il dit seulement que les longueurs AE et HE croissent à la même vitesse. En outre il est tout à fait possible de justifier le raisonnement de Roberval à l'aide du calcul différentiel.
Une justification analytique : Montrer
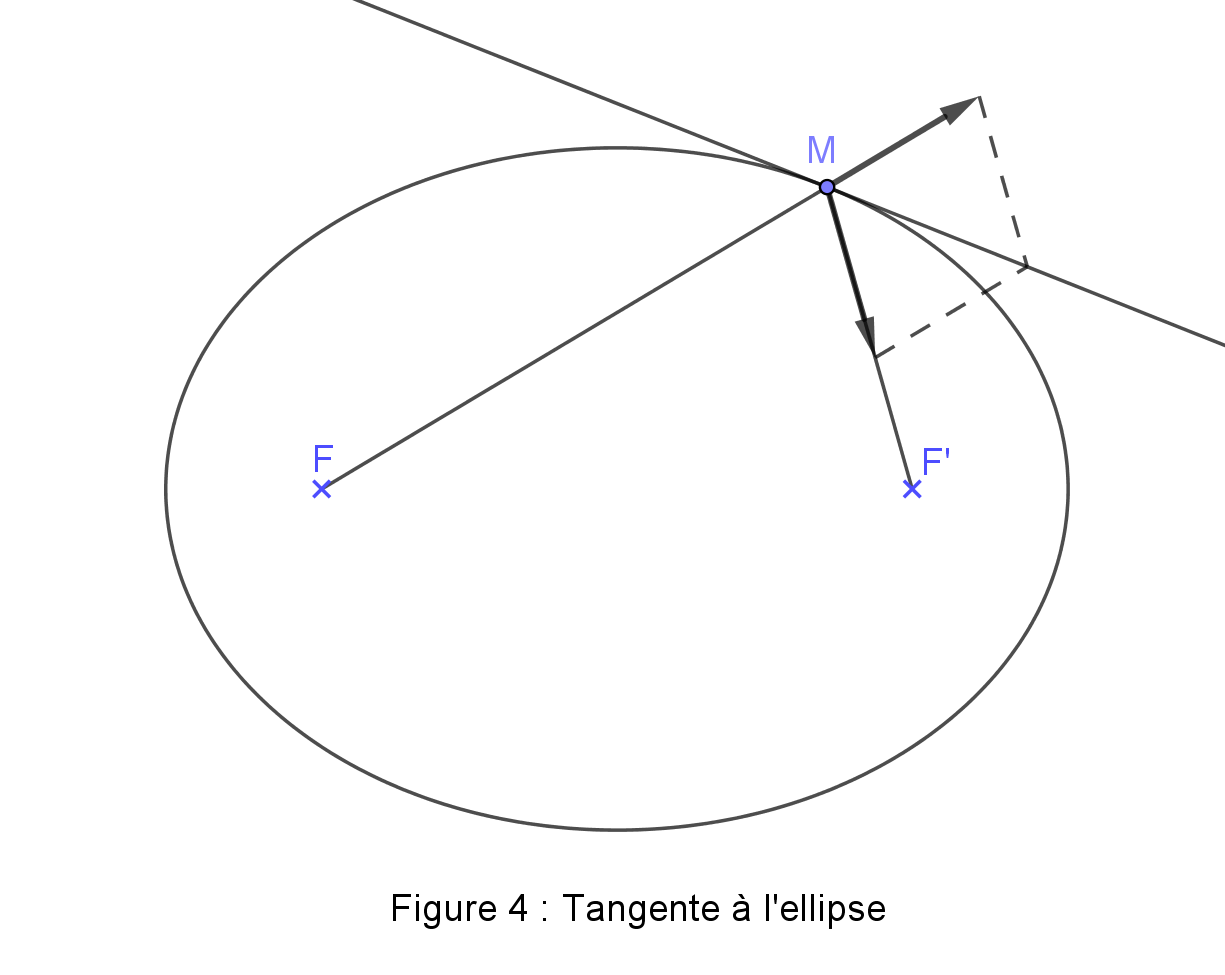
Roberval traite le cas des tangentes à l'ellipse ou à l'hyperbole de façon analogue à celui de la parabole. Par exemple il explique que le mouvement d'un point M décrivant une ellipse de foyers F et F' est composé de deux mouvements droits égaux, l'un selon MF, l'autre selon MF'. Les vitesses de ces deux mouvements sont toujours égales car la somme MF + MF' est constante. Il en résulte immédiatement que la tangente en M à l'ellipse est la bissectrice extérieure de l'angle FMF' (figure 4).
On voit que c'est la possibilité de trouver deux directions de droite suivant lesquelles les composantes du vecteur vitesse sont de même norme qui rend la méthode de Roberval d'une utilisation aussi simple dans le cas des coniques. Lorsque cette possibilité est absente Roberval doit faire preuve d'ingéniosité comme nous allons le voir avec l'étude des tangentes à la conchoïde de Nicomède.
Après avoir rappelé la construction point par point de la courbe de Nicomède Roberval considère que « la conchoïde est décrite par deux mouvements du même point ; l'un par lequel il monte le long de la ligne DF ; l'autre par lequel la ligne DF se mouvant circulairement sur le centre D, emporte le même point de C par F vers K » (ibid. p.34-35). L'animation ci-dessous illustre les propos de Roberval.
Conchoide de Nicomède : Montrer l'animation
Il explique que les directions de ces mouvements sont connues (la ligne DF pour le mouvement rectiligne, la droite FK perpendiculaire à DF pour le mouvement circulaire), mais que le rapport de leurs vitesses (voir note 4) ne l'est pas. Il faut alors, dit-il, « examiner ou les mêmes mouvements ou d'autres qui leur soient proportionnés hors de la conchoïde ». Or, poursuit-il, il est très facile d'examiner le mouvement du point G intersection de la droite DF avec la base AB. En effet le mouvement de ce point G, qui décrit la droite AB, est composé, lui aussi, d'un mouvement rectiligne suivant DF et d'un mouvement circulaire autour de D. Et comme les directions de ces deux mouvements et de leur composé sont connues, le rapport de leurs vitesses l'est aussi (voir note 5). En vertu des principes de sa méthode, Roberval peut affirmer que celui-ci est égal à GH/HI où GH est un segment perpendiculaire à DF et I le point de la droite AB tel que les droites HI et DG soient parallèles. (Figure 5)
Pour en déduire la direction du mouvement du point F sur la conchoïde, Roberval fait remarquer que, premièrement le mouvement rectiligne de F (selon DF) est égal à celui de G puisque la distance GF est constante, et deuxièmement que les mouvements circulaires de F et de G (autour de D) sont dans le même rapport que les rayons DF et DG. On obtiendra donc la direction du mouvement de F en construisant le point K sur la droite DH tel que les droites FK et DF soient perpendiculaires, puis le point L tel que les segments KL et HI soient parallèles et de même longueur.
La démarche précédente peut laisser le lecteur moderne dubitatif. Cependant, pour reprendre les termes de Gaspard Monge (cf. citation en tête d'article), elle est implicitement comprise dans les procédés du calcul différentiel, et dans le cas de la conchoïde l'analogie avec le calcul de l'expression du vecteur vitesse en coordonnées polaires est frappante.
Calcul en coordonnées polaires : Montrer
Notes
- La Société royale de Londres fut fondée le 28 novembre 1660 au Gresham College ; l'Académie des sciences de Paris fut créée par Colbert en 1666 ; celle de Berlin en 1700 par Frédéric I.(Retour au texte)
- Le réseau des savants correspondants de Mersenne comportait entre autres : Cavalieri, Cavendish, Desargues, Descartes, Fermat, Frenicle, Galilée, Huygens, Mydorge, Etienne Pascal, Pell, Roberval, Grégoire de Saint Vincent, Torricelli. Mersenne organisait également des réunions savantes à Paris au couvent des minimes près de la place royale.(Retour au texte)
- Le lecteur intéressé en trouvera un exemple dans Mathématiques au fil des âges (cf. biblio 3). (Retour au texte)
- Roberval utilise l'expression : "la raison d'un mouvement à un autre".(Retour au texte)
- En effet il suffit de construire un triangle dont les côtés ont pour direction celle des deux mouvements et de leur composé, la longueur des côtés sera alors proportionnelle à la vitesse de ces mouvements.(Retour au texte)
Bibliographie
- [ROB] Roberval, Gilles Personne de. Divers ouvrages in Mémoires de l'Académie Royale des Sciences depuis 1666 jusqu'à 1699, t. VI, Paris 1730.
- [GAL] Galilée. Discours concernant deux sciences nouvelles. Introduction, traduction, notes et index par Maurice Clavelin. Presses Universitaires de France, Paris 1995.
Textes originaux cités
- Collette Jean-Paul Histoire des mathématiques tome 1. Editions du Renouveau Pédagogique Inc., Montréal, 1973. Diff. Vuibert, Paris
- Dugas René. Histoire de la mécanique. Editions du Griffon, Neuchâtel, 1950 (réed. Gabay, 1996).
- I.R.E.M. Groupe Epistémologie et Histoire. Mathématiques au fil des âges. Gauthier-Villars, Paris, 1987.
Autres ouvrages