Les sona du peuple Chokwe
Souvent nous avions vu des jeunes enfants assis en cercle jouant avec le sable, et un jour profitant d’un moment de loisir je m’approchai d’eux et m’enquis de ce qu’ils faisaient. Comme j’étais devenu ami de certains d’entre eux, ils m’invitèrent à m’asseoir. […] Les enfants étaient en train de dessiner, et ils me demandèrent immédiatement d’effectuer des tâches impossibles ; grande fut leur joie lorsque l’homme blanc échoua à les accomplir. Dessine ce dessin sans lever ton doigt ! Et celui-ci ! A la fin on me montra, et je fis les croquis suivants de ce que j’avais appris. (Emil Torday, On the trail of the Bushongo, 1925)
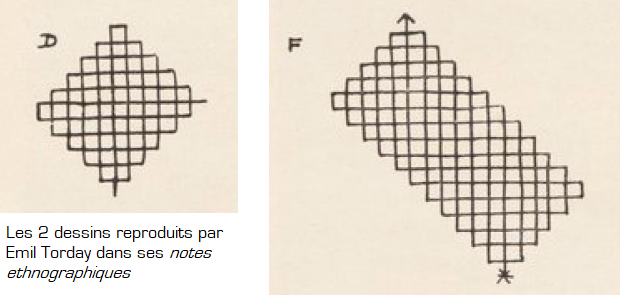
source : gallica.bnf.fr / Bibliothèque de l’INHA / coll. J. Doucet
Cette anecdote est rapportée par l’ethnologue hongrois Emil Torday qui au début du 20e siècle visita le sud du Congo (alors sous domination coloniale de la Belgique) pour rencontrer les peuples Kuba dont font partie les Bushongo.
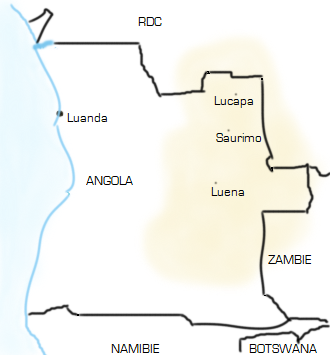
dessin 1
La tradition des dessins sur sable est très répandue dans cette région de l’Afrique centrale. Les plus remarquables de ces œuvres éphémères sont celles des Lunda Chokwe, un autre peuple bantou voisin des Bushongo, dont l’ère culturelle s’étend sur l’Est de l’Angola et les régions limitrophes de la république démocratique du Congo et de la Zambie. (cf. dessin 1)
Une pratique culturelle
Pour le peuple Chokwe, ces dessins qu’ils appellent sona sont plus qu’un simple jeu. Ils remontent à une tradition très ancienne et peuvent se rapporter à des animaux, des proverbes, des fables, des mythes. Ils jouent un rôle important dans la transmission du savoir et de la sagesse.
Les jeunes apprenaient la signification et l’exécution des sona les plus simples lors de la mukanda (rite d’initiation). Les plus difficiles n’étaient maîtrisés que par les akwa kuta sona (maîtres du dessin) qui formaient une élite au sein des Chokwe. Le tracé des lignes devait être exécuté rapidement et sans interruption pour être considéré comme parfait. Cette pratique culturelle est toujours vivante de nos jours en partie grâce à leur utilisation dans des établissements d’enseignement. Elle a été inscrite récemment en 2023 au patrimoine culturel immatériel de l’humanité.
Il existe des centaines de sona différents. Les dessins 2 & 3 en représentent quelques exemples simples à réaliser.
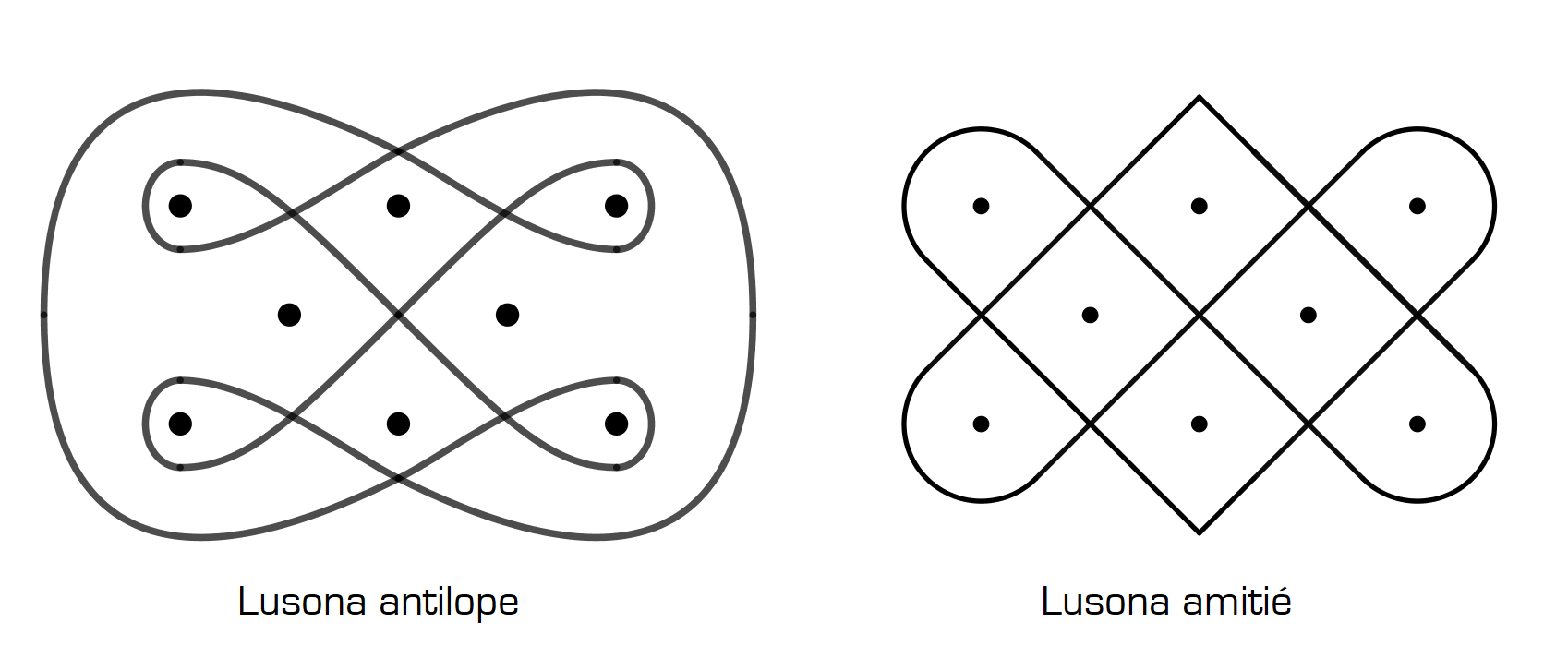
dessin 2
Pour commencer le dessinateur marquait un réseau de points dans le sable, puis il dessinait le lusona (sona se dit au pluriel, lusona au singulier) en traçant une ou plusieurs lignes continues entourant les points.

dessin 3
Les sona forment souvent le support d’un récit. Dans la tradition le récit accompagne la réalisation du lusona. Celui-ci s’appelle le serpent et le nid d’hirondelle :
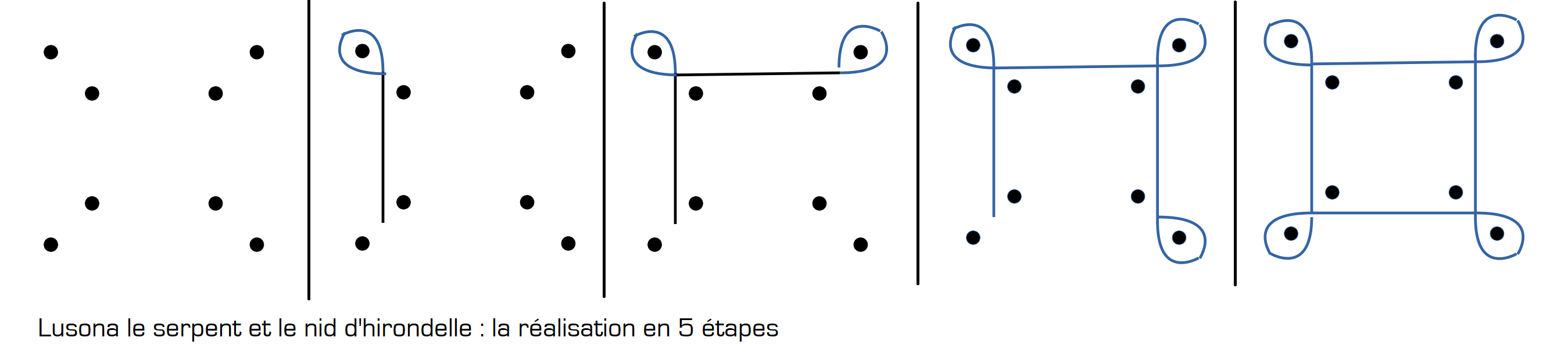
dessin 4
Une hirondelle avait construit son nid entre les quatre branches d’un arbre. Un serpent entendit le cri des oisillons et décida d’aller les voir. Il rampa tout près du nid et s’enroula autour de la première branche. Il poursuivit son chemin et tourna autour des la deuxième branche, puis de la troisième et de la quatrième. Maintenant il était revenu à son point de départ. Il continua ainsi à tourner autour des quatre branches pendant des jours. Jusqu’à ce qu’il n’entende plus les oisillons et se décide à aller voir ce qui était arrivé. Il entre alors dans le nid et le trouve vide !
Le regard du mathématicien
Comme dans la plupart des œuvres artistiques des peuples premiers la symétrie est présente dans de très nombreux sona (axes vertical et/ou horizontal le plus souvent et parfois des symétries de rotation). Les exemples ne manquent pas dans cet article. On peut noter que les sona trace d’antilope et tam tam sont identiques à un quart de tour près mais n’ont pas la même signification. Certains sona comme les trois oiseaux kumbi sont obtenus par répétition d’un même motif.

dessin 5
La propriété la plus remarquable de la majorité des sona est d’être monolinéaires, ce qui signifie qu’ils ont été réalisés en traçant une seule courbe continue. Cette caractéristique était sans aucun doute très recherchée par les maîtres du dessin. C’est le cas de tous les exemples précédents y compris celui du rat si l’on ne tient pas compte du tracé de la tête et de la queue. (cf. dessin 5)
Il existe cependant des sona dont le tracé utilise plusieurs courbes. Ainsi le lusona évoquant un esprit qui mange des fourmis est réalisé en traçant deux courbes fermées (cf. dessin 6).
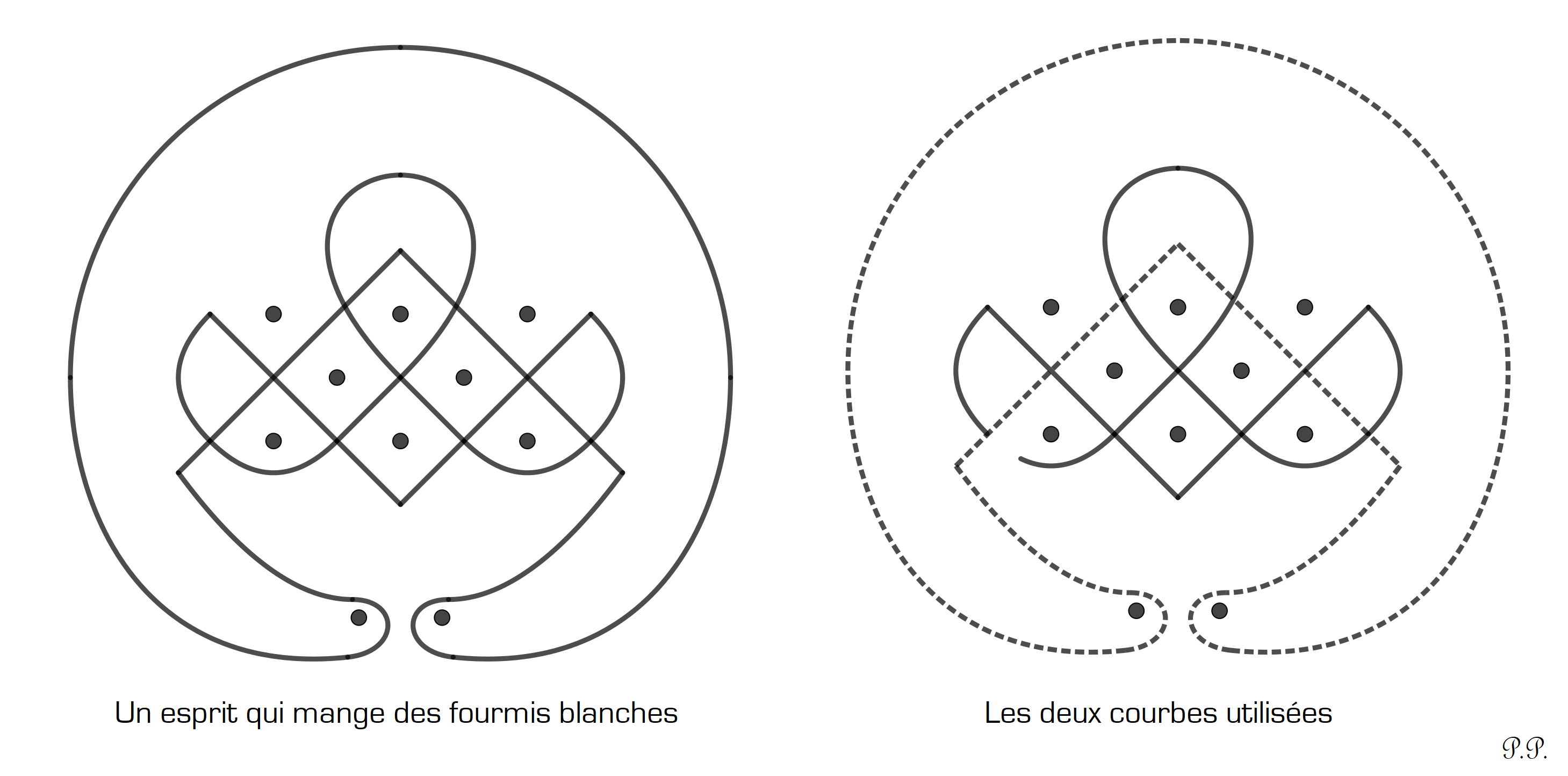
dessin 6
Parfois c’est une propriété topologique du dessin qui est utilisée pour illustrer l’histoire associée ; comme pour le lusona associé à la mukanda, le rituel d’initiation des garçons (cf. dessin 7). Ce rituel concernait les jeunes adolescents de 9 à 15 ans, qui étaient amenés loin de leurs parents dans un campement de brousse pendant plusieurs mois (voire plusieurs années). Après la circoncision ils apprenaient les règles de la communauté et les mythes de leur culture et s’exerçaient à différentes activités manuelles. Le lusona représente le campement, les 6 points au centre les garçons, les deux points en haut deux masques rituels gardiens du camp et les deux points du bas deux personnes non concernées par le rituel. Ces deux derniers sont placés à l’extérieur du campement pour illustrer la séparation des initiés du reste de la communauté pendant toute cette période.
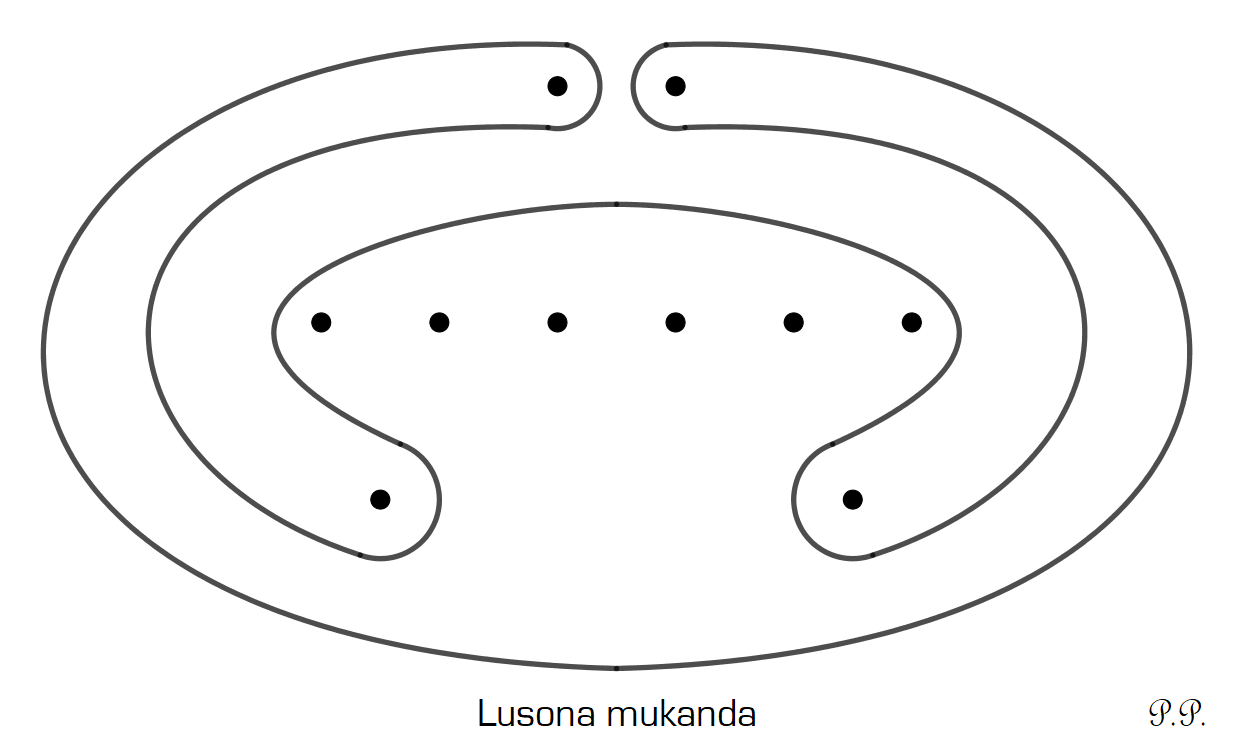
dessin 7
Les motifs de « bandes tressées »
Paulus Gerdes a étudié les propriétés mathématiques de centaines de sona et a remarqué qu’un motif particulier revenait souvent. Il s’agit de celui des bandes tressées ainsi nommé par analogie avec la technique de vannerie utilisée pour réaliser des paniers (cf. photo ci-après).

motif de bandes tressées
Voici deux variantes de ce motif de bandes tressées dessinées autour d’un réseau de 8 points (2 rangées de 3 points formant 2 carrés et les centres des 2 carrés)
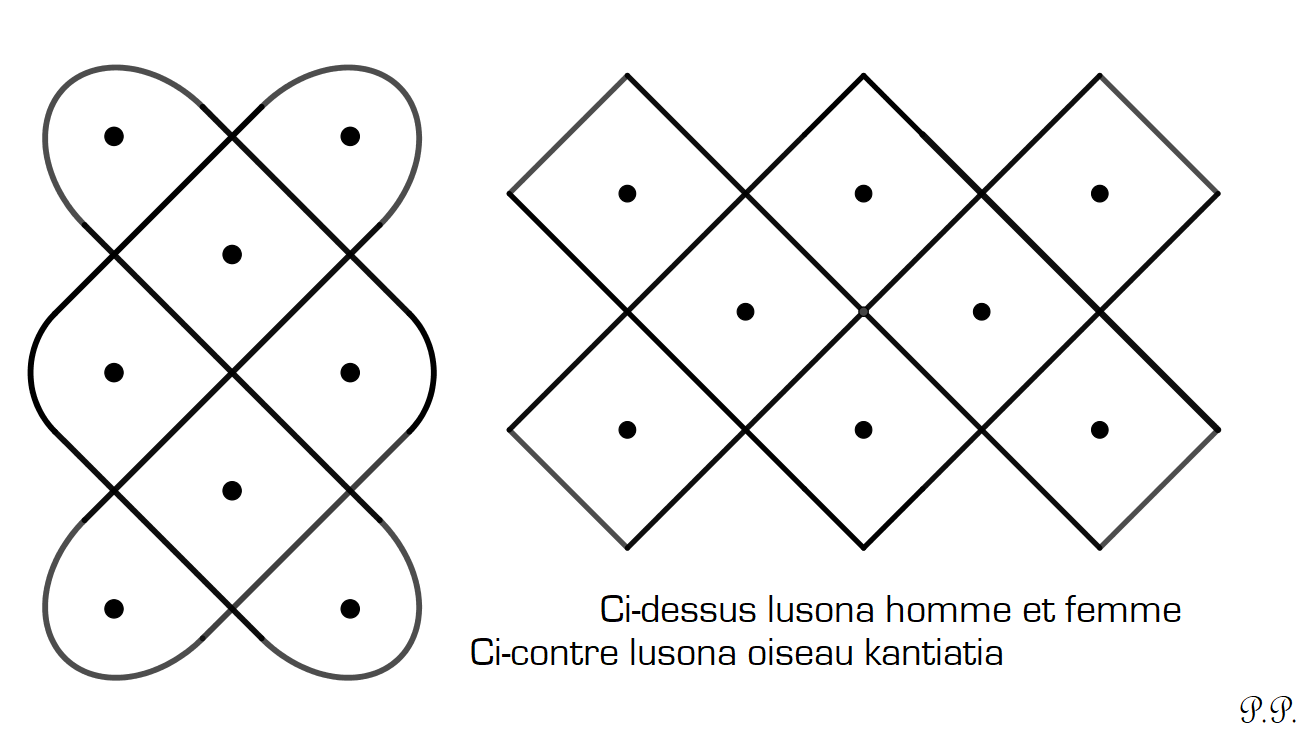
dessin 8
Dans un motif de bandes tressées les « bords » peuvent être arrondis ou à angle droit selon la signification du dessin : le lusona amitié (dessin 2) est une autre variante du motif précédent. On remarquera que, parmi les exemples de sona déjà donnés, le rat et l’oiseau mbemba sont construits à partir de motif de bandes tressées 3 × 2 en ajoutant deux éléments figuratifs de l’animal.
Ci-dessous deux autres sona construits à partir d’un motif de bandes tressées : le premier utilise un réseau 3 × 3 (3 rangées de 3 points formant 4 carrés), le second un réseau 4 × 3 (3 rangées de 4 points formant 6 carrés)
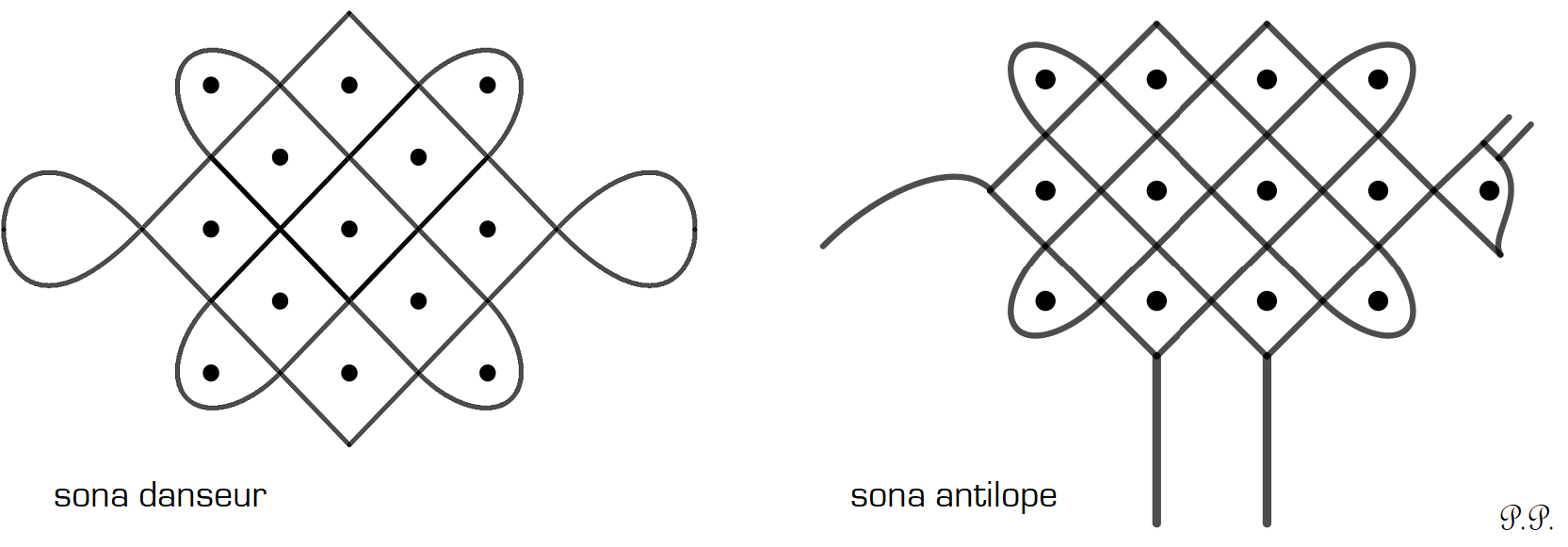
dessin 9
On peut remarquer que les sona construits à partir d’un motif 3 × 2 ou 4 × 3 sont monolinéaires, mais que
le lusona construit à partir d’un motif 3 × 3 utilise 3 courbes. Derrière cette simple constatation se cache
une propriété générale qui est l’objet d’une étude détaillée dans la version pdf de cet article. Tous ces sona peuvent
être tracés en suivant une procédure assez simple qui est également décrite dans la version pdf.
Les dessins reproduits par Emil Torday sont également des exemples de motif de bandes tressées de taille
plus importante, mais sans réseau de points apparent (ce réseau est en fait d’un type différent
des précédents).
Terminons cette présentation avec deux de mes sona préférés.
Kalunga ou le commencement du monde
Le dessin 10 reproduit le lusona appelé le dieu Kalunga. Ce lusona est associé à un récit mythologique
du peuple Chokwe qui explique le cycle du soleil et de la lune ainsi que la condition de simples mortels
des humains. (Ce récit est donné dans la version pdf).
Le dieu Kalunga est représenté en haut, le soleil à gauche, la lune à droite et l’homme en bas.
Le dessin est monolinéaire et s’appuie sur un réseau de 36 points. Il possède un axe de symétrie vertical ;
chacune des parties gauche et droite possède un axe de symétrie horizontal et leur tracé repose sur un motif
triangulaire de bandes tressées. Ces deux parties sont reliées en un seul point. En partant de ce point dans
la direction Sud Ouest on parcourt toute la partie gauche avant d’y revenir et de parcourir toute la partie
droite.
dessin 10
La poule en fuite
Le dessin 11 reproduit un lusona remarquable tant par l’originalité de son tracé que par sa puissance évocatrice. Il représente le trajet d’une poule sauvage qui est poursuivie. Il est monolinéaire, ne possède pas d’axe de symétrie mais est invariant par symétrie centrale. Il s’appuie sur un réseau orthogonal de 30 points équidistants mais utilise un algorithme de tracé de la ligne continue bien plus complexe que celui des motifs de bandes tressées.
dessin 11
Des artistes mathématiciens
Longtemps les Européens n’ont vu chez les peuples premiers que des sauvages incapables d’avoir par eux-mêmes une pensée rationnelle très élaborée. Il a fallu attendre le milieu du 20e siècle avec l’accumulation des données ethnographiques et le développement de l’ethnologie pour que le regard de l’occident sur les sociétés indigènes évolue. Pour peu qu’on accepte de prendre ses distances par rapport au savoir occidental traditionnel, on peut découvrir chez les peuples premiers des compétences mathématiques insoupçonnées. Ainsi chez les Chokwe les maîtres du dessin connaissaient plusieurs formes de symétrie, recherchaient la monolinéarité des tracés de sona, utilisaient certaines propriétés topologiques des courbes, inventaient des algorithmes pour réaliser les sona les plus complexes. Alors oui les akwa kuta sona étaient aussi bien mathématiciens qu’artistes.
A propos des illustrations
A l’exception des reproductions des deux dessins d’Emil Torday en début d'article toutes les illustrations (dessins de sona, photo de bandes tressées, carte du pays Chokwe) ont été réalisés par l’auteur. L’utilisation d’un logiciel fournit des dessins idéalisés de sona qui soulignent les propriétés de symétrie au détriment de la propriété de monolinéarité quand elle est présente. Pour mieux se rendre compte de la difficulté que représente la réalisation d’un lusona il faut essayer par soi-même de tracer chaque courbe continue sans lever la main et sans s’arrêter. On pourra alors apprécier toute l’habilité des akwa kuta sona. On peut aussi voir un de ces artistes à l’œuvre dans une video sur le site du patrimoine immatériel de l’UNESCO (ici).
Bibliographie
- Marcia Ascher, Mathématiques d’ailleurs, Editions du Seuil, 1998.
- Paulus Gerdes, Une tradition géométrique en Afrique les dessins sur le sable, L’Harmattan,Paris, 1995.
- Paulus Gerdes, On mathematics in the history of sub-saharan Africa, in Historia Mathematica 21, 1994.
- Paulus Gerdes, Les sona : des graphes sur le sable angolais, in Pour la Science dossier n° 47 : Mathématiques exotiques, 2005.
- Emil Torday, On the trail of the Bushongo, Seeley, London, 1925. Disponible sur Internet Archive
- Emil Torday & T. A. Joyce, Notes ethnographiques sur les peuples communément appelés Bakuba, ainsi que sur les peuplades apparentées. Les Bushongo, in Annales du Musée du Congo Belge, 1910. Disponible sur Gallica
- Claudia Zaslavsky, Math Games & Activities from around the world, Chicago Review Press, 1998.
Sites consultés
- Sona, dessins et figures géométriques sur le sable - patrimoine immatériel - secteur de la culture - Unesco
- Les objets rituels de l’initiation mukanda au Royal Museum for central Africa (Teruven, Belgique)