Courbes et Tangentes dans les Mathématiques Grecques II


Les acteurs principaux

La spirale d'Archimède

Archimède notice biographique : Montrer

De l'avis des historiens, Archimède est sans doute l'inventeur de la spirale qui porte son nom. Il a consacré un traité entier à l'étude de ses propriétés. Cette courbe est l'un des deux exemples de courbes transcendantes envisagées par les Grecs (l'autre est la quadratrice) et en dehors des coniques, c'est la seule courbe dont ils aient déterminé les tangentes.

Archimède donne une définition cinématique de sa spirale :

Si une ligne droite est menée dans un plan, et si, l'une de ses extrémités restant fixe, elle tourne un nombre quelconque de fois d'un mouvement uniforme, reprenant la position d'où elle est partie, tandis que, sur la ligne en rotation, un point se meut uniformément comme elle à partir de l'extrémité fixe, le point décrira une spirale dans le plan. ([ARC], t.1, p.261)

Spirale d'Archimède : Montrer l'animation

Après avoir établi quelques propriétés de la courbe que nous traduisons maintenant par l'équation en coordonnées polaires (ρ = kθ), Archimède s'intéresse à la détermination des tangentes à travers trois propositions.

La première concerne la tangente au point atteint après la première révolution (figure 10).

Proposition 18 : Si une ligne droite est tangente à l'extrémité d'une spirale décrite en première révolution, et, si du point d'origine de la spirale, on élève une perpendiculaire sur la droite initiale de révolution, cette perpendiculaire rencontrera la tangente, tandis que la droite, située entre la tangente et l'origine de la spirale, sera égale à la circonférence du premier cercle. ([ARC], t.1, p.269)

Commentaire : Dans la figure 10, le point B est l'extrémité de la spirale. (AB) est la droite initiale, et (AZ) la perpendiculaire. La longueur AZ est égale à la circonférence du cercle de centre A et de rayon AB, appelé premier cercle.

Archimède donne ensuite la tangente au point atteint après deux révolutions (cf. figure 11), avant de traiter le cas général d'un point quelconque atteint pendant la première révolution.

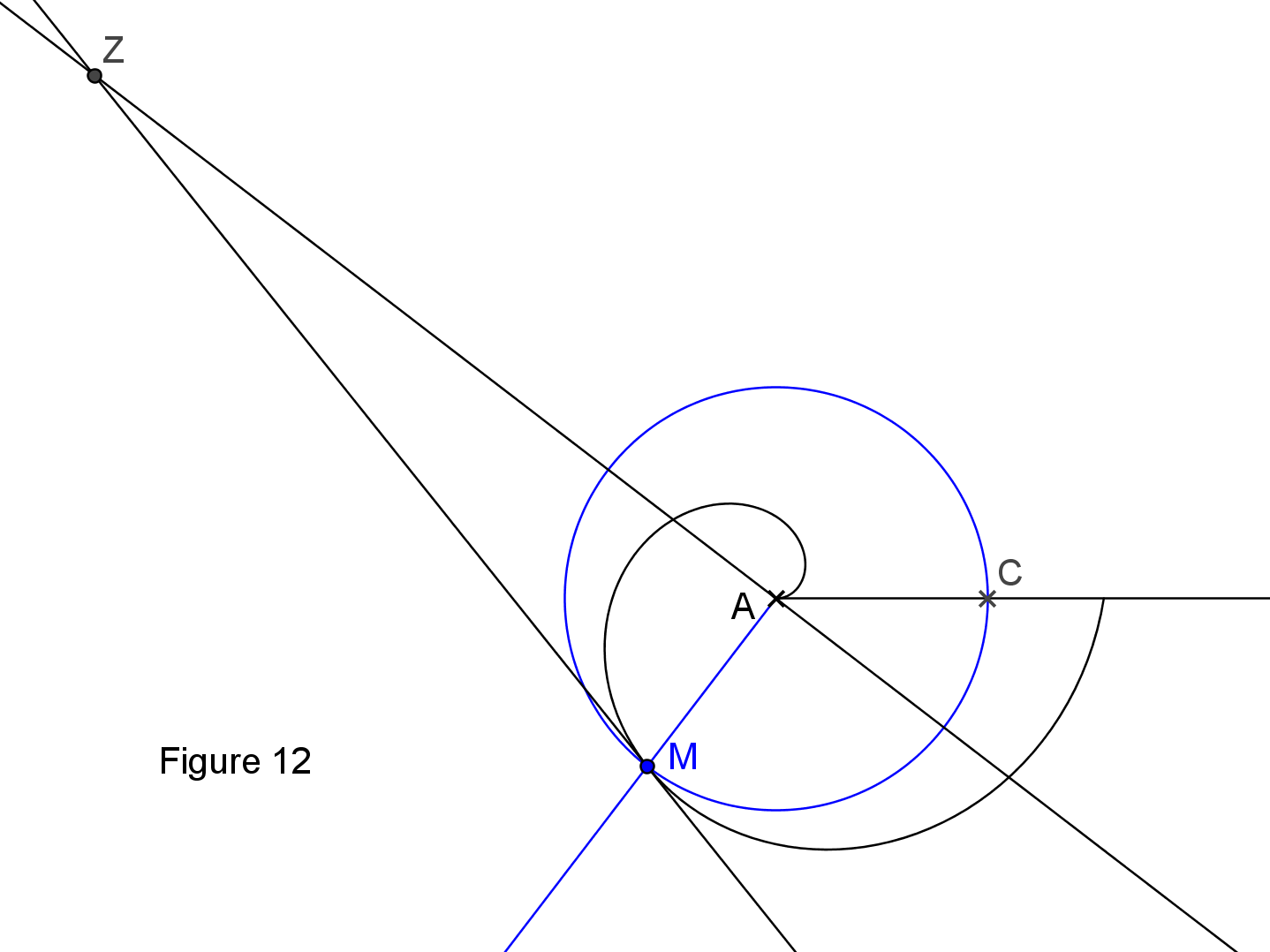
Proposition 20 : si une droite est tangente à une spirale décrite en première révolution, sauf à l'extrémité de cette spirale ; si une droite relie le point de contact avec l'origine de la spirale ; si un cercle est décrit de l'origine de la spirale comme centre avec la droite de jonction comme rayon, et, si une perpendiculaire est menée de l'origine de la spirale sur la droite reliant le point de contact avec l'origine de la spirale, cette perpendiculaire rencontrera la tangente, tandis que la droite située entre le point de rencontre et l'origine de la spirale sera égale à l'arc du cercle décrit, situé entre le point de contact et le point d'intersection où le cercle décrit coupe la ligne initiale de révolution ; cet arc étant pris vers l'avant, à partir du point situé sur la droite initiale de révolution.  ([ARC], t.1, p.275)

Commentaire : Dans la figure 12, le point de contact est M. Le cercle décrit a pour centre A et pour rayon AM. Les droites AM et AZ sont perpendiculaires. Le segment AZ a la même longueur que l'arc de cercle CM pris dans le sens de révolution. La figure a été tracée avec (AC) comme position initiale de la droite qui tourne dans le sens trigonométrique.

Archimède démontre les propositions précédentes de manière rigoureuse par des considérations purement géométriques, son argumentation repose à chaque fois sur un double raisonnement par l'absurde consistant à prouver que la distance AZ ne peut être ni plus grande, ni plus petite que la longueur annoncée. En revanche il n'indique pas par quel procédé il a trouvé la position de la tangente dont il admet l'existence. On verra dans le chapitre suivant que le principe de composition des mouvements permet de la déterminer facilement. Mais Archimède avait-il quelque idée de celui-ci ?

Retenons que pour les mathématiciens grecs la tangente est une droite qui, au moins localement, est tout entière d'un même côté de la courbe. Par conséquent, démontrer qu'une droite passant par un point d'une courbe lui est tangente, revient à établir certaines inégalités.

En appendice à ce chapitre, nous allons présenter trois autres courbes que les géomètres grecs rencontrèrent à l'occasion de leurs célèbres problèmes de construction. Comme ils ne réalisèrent pas la détermination de leurs tangentes, elles firent naturellement partie des premiers exemples sur lesquels les mathématiciens du 17e siècle mirent à l'épreuve leurs nouvelles méthodes.

Le premier de ces problèmes est celui des deux moyennes proportionnelles : étant donnés deux segments de longueur a et b, construire deux autres segments de longueur x et y tels que a⁄x = x⁄y = y⁄b .

En termes modernes a, x, y & b forment une progression géométrique.
Cette question très générale inclut celle de la duplication du cube (construire un cube de volume double d'un cube donné), qui en est le cas particulier lorsque b = 2a.

Les deux autres problèmes sont la trisection de l'angle (construire un angle égal au tiers d'un angle donné) et la quadrature du cercle (construire un carré dont l'aire est égale à celle d'un cercle de rayon donné). La difficulté de ces problèmes de construction réside dans le fait qu'ils ne sont pas résolubles à la règle et au compas (c'est-à-dire en n'utilisant que des droites et des cercles). Pour les résoudre les mathématiciens grecs ont donc été amenés à inventer d'autres courbes ou d'autres instruments ...


La conchoïde de Nicomède

On ne possède aucun écrit de Nicomède et aucun renseignement biographique précis. Ses travaux ont été mentionnés par Proclus, Eutocius et Pappus qui vécurent au 4e et au 5e siècle. Par recoupement des données les historiens estiment qu'il vécut au 3e siècle avant notre ère.

Dans ses commentaires sur le traité De la sphère et du cylindre d'Archimède, Eutocius rapporte une dizaine de manières de résoudre le problème des deux moyennes proportionnelles dont celle de Nicomède. Eutocius explique comment Nicomède a décrit, dans son ouvrage sur les conchoïdes, un instrument permettant de construire une solution au problème des moyennes proportionnelles. La figure ci-dessous (extraite des planches de l'Encyclopédie méthodique) présente cet instrument qui permet de tracer une branche de conchoïde.

L'instrument comporte donc trois règles. Deux règles fixées entre elles à angle droit pour former un T ; sur la règle "horizontale" (AD) est creusée une rainure en queue d'aronde dans laquelle peut se mouvoir un curseur ; sur la règle verticale est fixé un clou (point K). La troisième règle comporte une incision sur une partie de sa longueur dans laquelle le clou K peut glisser librement, de plus elle est fixée au curseur et un crayon traceur est situé à son extrémité (point C).

Conchoide de Nicomède : Montrer l'animation

Voici une définition mathématique correspondant au tracé instrumental précédent. Sont donnés une droite δ, un point O situé à une distance a de la droite δ et une longueur h. On considère une demi droite d'origine O qui coupe la droite δ en un point P. Sur cette demi droite et au-delà de P on place le point M tel que  PM = h (figure 13). Le lieu décrit par le point M lorsque la demi droite tourne autour de O est la conchoïde de Nicomède (de pôle O, de base δ et d'intervalle h).

Si l'on choisit le repère orthonormé direct d'origine O dans lequel le projeté orthogonal E de O sur δ a pour coordonnées (0 ; a), cette courbe admet pour équation polaire : ρ = h + a⁄sinθ ; 0 < θ < π

C'est l'une des deux branches de la quartique d'équation : (x - a)2 (x2 + y2) - h2x2 = 0.

Regardons maintenant comment Nicomède résoud le problème des deux moyennes proportionnelles à l'aide de la conchoïde. Voici la description de la construction rapportée par Eutocius d'Ascalon :

Ces choses étant démontrées, soient ΓΛ, ΛA deux droites perpendiculaires entre elles dont il faut trouver deux moyennes proportionnelles en proportion continue. Complétons le parallélogramme ABΓΛ ; divisons chacune des droites AB, BΓ, en deux parties égales aux points Δ, E ; menons la droite de jonction ΔΛ ; prolongeons-la et qu'elle rencontre la droite ΓB au point H. Menons la droite EZ à angles droits sur la droite BΓ ; menons la droite ΓZ égale à la droite AΔ ; menons la droite de jonction ZH ; menons la droite ΓΘ parallèle à celle-ci, et ayant l'angle compris sous les droites KΓ, ΓΘ, menons, du point donné Z, la droite ZΘK faisant la droite ΘK égale à la droite AΔ et à la droite ΓZ ; car il a été démontré que cela est possible au moyen de la conchoïde. Prolongeons la droite de jonction KΛ, et qu'elle rencontre au point M la droite AB prolongée. Je dis que la droite KΓ est à la droite MA et la droite MA à la droite AΛ comme la droite ΛΓ est à la droite KΓ. ([ARC], t.2, p.618-619)

Commentaire : tous les points de la figure à l'exception du point K peuvent être construits à la règle et au compas. Le point K se trouve à l'intersection de la droite BΓ et de la conchoïde de pole Z, de base la parallèle à (HZ) passant par Γ et de paramètre égal à AΔ.

Preuve de la solution de Nicomède : Montrer

La conchoïde de Nicomède permet également de résoudre le problème de la trisection de l'angle. En effet pour partager en trois un angle donné AOB du triangle rectangle OAB, il suffit de trouver un point M sur la parallèle à la droite OA passant par B tel que, si P désigne le point d'intersection des droites OM et AB, PM = 2OB (figure 15).

En effet, si I désigne le milieu du segment PM, en raison des triangles isocèles OBI et BIM, l'angle MOB sera le double de l'angle OMB, et par conséquent l'angle AOB sera le triple de l'angle AOM. Or la condition PM = 2OB sera réalisée si M appartient à la conchoïde de Nicomède de pole O, de base AB et d'intervalle 2OB (représentée en bleu sur la figure 15).


La cissoïde de Dioclès

Dioclès aurait vécu au 2e siècle avant notre ère. D'après Eutocius il est l'auteur d'un ouvrage sur les Miroirs ardents (qui ne nous ait pas parvenu) dans lequel il expose une solution au problème des deux moyennes proportionnelles à l'aide d'une courbe qui fut appelée plus tard cissoïde.

Etant donnés un cercle de diamètre AB = 2a et sa tangente en B, on considère une demi droite d'origine A qui recoupe le cercle au point P et la tangente au point N. Sur cette demi droite on place le point M tel que : AM = PN. La cissoïde de Dioclès est le lieu décrit par le point M lorsque la demi droite tourne autour de A (figure 16).

Cissoide de Dioclès : Montrer l'animation

Dans le repère orthonormé direct d'origine A dans lequel B a pour coordonnées (0 ; -2a), cette courbe admet pour équation polaire :

ρ = -2a cos2(θ)  ; -π < θ < 0
sin(θ)

Et pour équation cartésienne : y3 + yx2 + 2ax2 = 0. C'est donc une cubique.

Considérons la figure 17 dans laquelle le point C appartient à la cissoïde relative au cercle de diamètre AG. La demi-droite GC recoupe ce cercle au point Q et sa tangente en A au point R. I et B et sont les projetés orthogonaux de Q et C sur le diamètre AG. Enfin H est l'intersection de (BC) avec le demi-cercle GQA. Nous allons montrer que les longueurs AB, BH, BG, BC forment une progression géométrique.

La première égalité AB ÷ BH = BH ÷ BG provient du fait que le triangle AHG est rectangle en H et que HB est une hauteur de ce triangle. D'autre part, AB = IG car GQ = CR et par conséquent les triangles ABH et GIQ sont symétriques par rapport au diamètre du cercle perpendiculaire à (AG). Il vient alors : AB ÷ BH = GI ÷ IQ = BG ÷ BC. CQFD.

Reste à voir maintenant comment on peut déduire de la propriété précédente une solution au problème des deux moyennes proportionnelles. Soient a et b (a < b) les deux nombres dont on cherche les moyennes proportionnelles. Sur la figure 18 on a tracé la cissoïde relative au cercle de diamètre AG. On place ensuite les points B' et C' tels que le triangle AB'C' soit rectangle en B avec AB' = a et B'C' = b. Soit C le point d'intersection de la cissoïde avec la droite AC'. On trace la parallèle à B'C' passant par C, elle coupe le segment AG en B et le demi-cercle de diamètre AG en H. D'après ce qui précède les longueurs AB, BH, BG, BC forment une progression géométrique. Il suffit donc de construire une longueur x et une longueur y telles que a ÷ AB = x ÷ BH = y ÷ BG et ainsi a, x, y, b formeront une progression géométrique (sur la figure 18, x = B'H' et y = B'G').

Il faut noter que les mathématiciens grecs n'ont pas donné de méthode de construction instrumentale de la cissoïde. Dioclès se contente de construire point par point un arc de la courbe située à l'intérieur du cercle. Il est néanmoins possible de décrire la cissoïde d'un mouvement continu comme Isaac Newton le montrera dans son Arithmetica universalis.


La quadratrice de Dinostrate

Cette courbe aurait été inventée par Hippias d'Elis (vers -400) pour résoudre la trisection de l'angle et aurait été employée par Dinostrate (4e siècle avant notre ère) pour résoudre le problème de la quadrature du cercle, d'où son nom. Voici la description qu'en donne Pappus. Soit un carré OBEC ; on suppose qu'un rayon [OD] se déplace autour de O dans un mouvement de rotation uniforme depuis [OC] jusqu'à [OB] et que dans le même intervalle de temps un segment QR se déplace dans un mouvement de translation uniforme depuis [CE] jusqu'à [OB]. La quadratrice est le lieu des points d'intersection des segments OD et QR (figure 19).

Quadratrice de Dinostrate : Montrer l'animation

Les points M de la quadratrice vérifient la relation MP ÷ OC = angle BOM ÷ angle BOC , où P désigne le projeté orthogonal de M sur la droite OB. On peut en déduire comme le rapporte Pappus que, si V est le point d'intersection de la quadratrice avec la droite OB, arc BDC ÷ OC = OC ÷ OV . Il serait donc possible à partir du segment OV de construire une solution au problème de la quadrature du cercle (voir ci-dessous).

Voici une démonstration moderne du résultat précédent. Notons r la longueur OC, θ l'angle BOM et (x , y) les coordonnées de M dans le repère orthonormé direct d'origine O dans lequel B a pour coordonnées (r , 0). De la relation : y ÷ r = 2θ ÷ π , on déduit l'équation cartésienne de la courbe : x = y cot(πy⁄2r) ; 0 < y ≤ r

Quand y tend vers 0, x tend vers 2r⁄π, par conséquent le point V (2r⁄π ,0) prolonge bien la courbe par continuité.

La quadrature du cercle à partir du segment OV : Montrer

Mais cette solution est purement théorique, ce que certains mathématiciens grecs avaient déjà pressenti. Voici une critique faite par Sporus et rapportée par Pappus : "comment est-il possible, avec deux points partant de C, de déplacer l'un le long d'une droite jusqu'à O et de déplacer l'autre le long d'un cercle jusqu'à B dans le même temps sans connaître en premier le rapport de la longueur du segment CO à la longueur de l'arc CB ? En fait ce rapport doit être également celui des vitesses des deux mouvements."
Autrement dit si l'on cherche à construire un instrument permettant de synchroniser le mouvement circulaire du point D avec le mouvement rectiligne du point Q (par exemple avec une crémaillère), il faut déjà connaître le rapport que l'on cherche à obtenir ! La quadratrice ne peut donner qu'une solution graphique approchée par exemple en construisant par bissection à la règle et au compas les points de celle-ci correspondants à θ = π÷2n.


Bibliographie

    Autres ouvrages

  1. Collette Jean-Paul Histoire des mathématiques tome 1. Editions du Renouveau Pédagogique Inc., Montréal, 1973. Diff. Vuibert, Paris
  2. Gomes Teixeira Francisco. Traité des courbes spéciales remarquables planes et gauches (3 tomes). Coïmbre, Imprimerie de l'Université, 1908 (réed. Gabay, 1995).
  3. Heath Thomas Sir. A history of greeks mathematics vol 1&2. Oxford, Clarendon Press, 1921.
  4. I.R.E.M. Groupe Epistémologie et Histoire. Mathématiques au fil des âges. Gauthier-Villars, Paris, 1987.
  5. Lebesgue Henri. Leçons sur les constructions géométriques. Gauthier-Villars, Paris, 1950 (réed. Gabay, 1987)
Image de fond : source gallica.bnf.fr/BnF