L'équation de Pell Fermat et les mathématiques indiennes
Trouver les solutions dans N×N de : nx² + 1 = y²
Méthode de Brahmagupta (7e siècle)
Qui était Brahmagupta ? Montrer
Brahmagupta (né en 598) astronome, mathématicien, est le plus connu des savants de l'école de Ujjain (Madhya Pradesh). Son ouvrage Brahmasphutasiddhanta contient les règles de calcul sur les nombres relatifs, les propriétés opératoires du zéro, ses travaux sur la résolution des équations indéterminés, sur les propriétés du quadrilatère inscriptible. C'est par une traduction de son œuvre que les Arabes prirent connaissance des mathématiques indiennes.
1) Si on connait un couple solution, on peut en trouver une infinité par la méthode de composition.
Exemple n°1 : l'équation 8x² + 1 = y² a pour solution évidente (1 ; 3)
On en obtient une autre en faisant " les produits en croix " : 1×3 + 3×1 qui donne la valeur de x (= 6) d'où l'on déduit la valeur de y (= 17).
On recommence en faisant " les produits en croix " avec les couples (1 ; 3) et (6 ; 17). On obtient x = 1×17 + 3×6 = 35 d'où y = 99.
On recommence en faisant " les produits en croix " avec les couples (1 ; 3) et (35 ; 99). On obtient x = 1×99 + 3×35 = 204 d'où y = 577.
L'explication repose sur l'identité de Brahmagupta :
(y² - nx²)(y'² - nx'²) = (nxx' + yy')² - n(xy' + yx')²
Elle prouve que si les couples (x ; y) et (x' ; y') sont solutions de l'équation de Pell Fermat, alors le couple (xy' + yx' ; nxx' + yy') la vérifie également.
2) Comment trouver une solution de l'équation de Pell Fermat par la méthode du Kuttaka.
Celle-ci consiste à construire une solution à partir de solutions " approchées " vérifiant nx² + a = y². Elle repose sur la remarque suivante conséquence de l'identité de Brahmagupta :
si le couple (x1 ; y1) vérifie l'équation nx² + a = y² et le couple (x2 ; y2) l'équation nx² + b = y²
alors le couple
(x1y2 + y1x2 ; nx1x2 + y1y2) vérifie l'équation nx² + ab = y².
Exemple n°2 : Résoudre l'équation 17x² + 1 = y²
(1 ; 4) vérifie l'équation 17x² - 1 = y² (solution " approchée "), donc (1×4 + 4×1 ; 17×1×1 + 4×4) = (8 ; 33) vérifie 17x² + 1 = y².
Exemple n°3 : Résoudre l'équation 27x² + 1 = y²
(1 ; 5) vérifie l'équation 27x² - 2 = y² (solution " approchée "), donc (1×5 + 5×1 ; 27×1×1 + 5×5) = (10 ; 52) vérifie 27x² + 4 = y². Mais 10 et 52 sont divisibles par 2 donc (5 ; 26) vérifie 27x² + 1 = y².
Remarque : Si le couple (x1 ; y1) vérifie l'équation nx² + a = y² avec a = 2 ou -2, alors le couple (2x1y1 ; nx1² + y1²) est solution de nx² + 4 = y² et nx1² + y1² est toujours divisible par 2 (car nx1² + y1² = 2nx1² + a). Brahmagupta sait également trouver une solution de l'équation de Pell Fermat à partir d'une solution approchée lorsque a = 4 ou -4.
Méthode de Bhaskara (12e siècle)
Qui était Bhaskara ? Montrer
Bhaskaracharya (né en 1114) appartient à l'école de Ujjain. Il représente l'apogée des mathématiques indiennes classiques. Ses travaux portent sur l'arithmétique, la combinatoire et l'algèbre. Par exemple il donne la solution entière minimale de l'équation : 61x² + 1 = y² (x = 226 153 980 et y = 1 766 319 049)
La méthode du chakravala améliore celle de Brahmagupta puisqu'elle permet de trouver la solution minimale dans tous les cas.
Exemple 4 : Résoudre l'équation 67x² + 1 = y²
Lemme : pour tout entier m le couple (1 ; m) vérifie 67x² + m² - 67 = y².
On part de la solution approchée (1 ; 8) : 67×1² - 3 = 8².
On cherche un entier m tel que le nombre m + 8 obtenu par " produits en croix " de (1 ; 8) et (1 ; m) soit divisible par -3 et que |m² - 67| soit minimal. On obtient m = 7. On sait alors que (15 ; 123) est solution de 67x² - 3×(-18) = y² d'où (5 ; 41) est solution de 67x² + 6 = y².
On recommence la même procédure avec (5 ; 41). L'entier m tel que le nombre 5m + 41 obtenu par " produits en croix " de (5 ; 41) et (1 ; m) soit divisible par 6 et que |m² - 67| soit minimal est m = 5. On sait alors que (66 ; 540) est solution de 67x² - 6×42 = y² et (11 ; 90) est solution de 67x² - 7 = y².
Encore une fois : l'entier m tel que le nombre 11m + 90 obtenu par " produit en croix " de (11 ; 90) et (1 ; m) soit divisible par -7 et que |m² - 67| soit minimal est m = 9.
On sait alors que (189 ; 1547) est solution de 67x² - 7×14 = y² et (27 ; 221) est solution de 67x² - 2 = y².
On peut alors trouver la solution minimale par la méthode de Brahmagupta, soit x = 27×221 = 5967 et y = 48 842.
Méthode d'Euler et Lagrange
La solution minimale de l'équation nx² + 1 = y² est donnée par le développement en fractions continues de √n (qui est périodique).
Qu'est-ce qu'un développement en fractions continues ? Montrer
Pour obtenir le développement en fractions continues d'un réel x, on définit deux suites an et bn comme suit :
a0 = x , b0 = [x] , et pour tout naturel n, an+1 = 1/(an - bn) et bn+1 = [an+1].
On démontre alors que la suite de rationnels (rn) définie comme suit converge vers le réel x.

Par exemple, le tableau suivant donne le développement en fraction continue (bn) et les réduites successives (rn) de √67. La solution minimale de l'équation 67x² + 1 = y² est donnée par le dénominateur et le numérateur de la dixième réduite.
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| bn = | 8 | 5 | 2 | 1 | 1 | 7 | 1 | 1 | 2 | 5 | 16 | 5 | 2 |
| num. de rn | 8 | 41 | 90 | 131 | 221 | 1678 | 1899 | 3577 | 9053 | 48842 | 790525 | 4001467 | 8793459 |
| dén. de rn | 1 | 5 | 11 | 16 | 27 | 205 | 232 | 437 | 1106 | 5967 | 96578 | 488857 | 1074292 |
On remarquera que les calculs par cette méthode sont plus longs que par celle de Brahmagupta et Bhaskara.
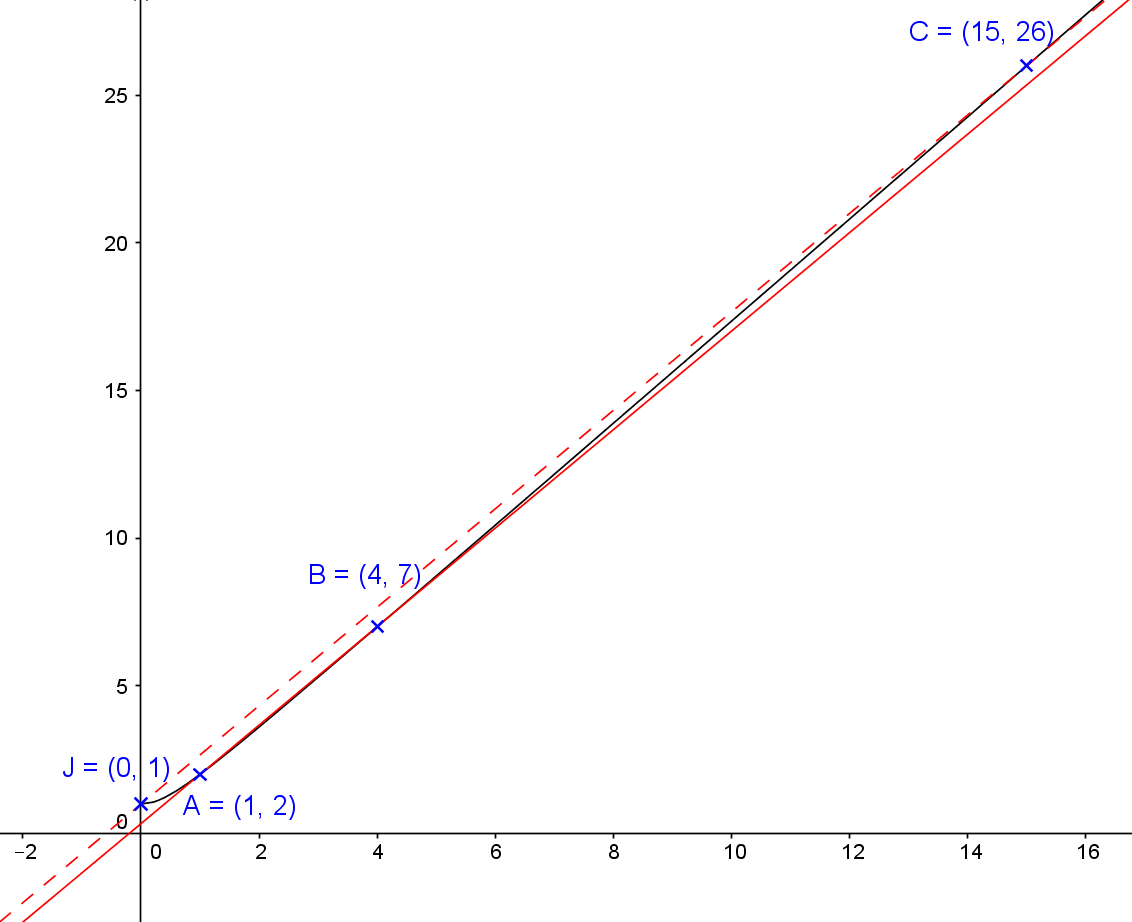
Une construction géométrique des solutions d'après l'identité de Brahmagupta
Les solutions de l'équation de Pell Fermat sont représentées par les points à coordonnées entières de l'hyperbole (Hn) : nx² + 1 = y².
En notant J(0 ; 1), M(x ; y), M'(x' ; y'), P(xy' + yx' ; nxx' + yy'), on vérifie que les droites (MM') et (JP) sont parallèles lorsque M et M' appartiennent à l'hyperbole (Hn). (Si M et M' sont confondues, la droite (JP) est parallèle à la tangente en M à l'hyperbole.)
Pour la figure on a pris n = 3. La solution minimale est (1 ; 2). Sachant que la droite JB est parallèle à la tangente en A, on obtient une deuxième solution (4 ; 7)
Sachant que la droite JC est parallèle à la droite AB, on obtient une troisième solution (15 ; 26).
Bibliographie
David, Marcel. Article Approximations Diophantiennes. Dictionnaire des Mathématiques. Encyclopedia Universalis/Albin Michel, Paris, 1997.
Joseph, George Gheverghese. The crest of the peacock. Penguin books, 1994.
Lagrange, Joseph Louis. Solution d'un problème d'arithmétique. Miscellanea Taurinensia, tome III, 1766-1769.
Stoltz, André. Equation de Pell-Fermat. L'ouvert 12, IREM de Strasbourg.